
如图,在平面直角坐标系中,点A(0,4),B(3,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,则直线BC的解析式为 .

科目:初中数学 来源: 题型:
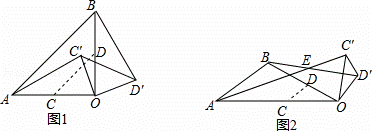
在△AOB中,C,D分别是OA,OB边上的点,将△OCD绕点O顺时针旋转到△OC′D′.
(1)如图1,若∠AOB=90°,OA=OB,C,D分别为OA,OB的中点,证明:①AC′=BD′;②AC′⊥BD′;
(2)如图2,若△AOB为任意三角形且∠AOB=θ,CD∥AB,AC′与BD′交于点E,猜想∠AEB=θ是否成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
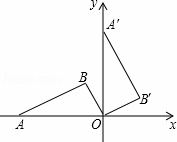
如图,在平面直角坐标系中,点A的坐标(﹣2,0),△ABO是直角三角形,∠AOB=60°.现将Rt△ABO绕原点O按顺时针方向旋转到Rt△A′B′O的位置,则此时边OB扫过的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
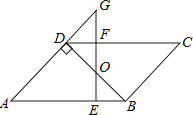
如图,▱ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
胡老师计划组织朋友暑假去革命圣地延安两日游,经了解,现有甲、乙两家旅行社比较合适,报价均为每人640元,且提供的服务完全相同,针对组团两日游的游客,甲旅行社表示,每人都按八五折收费;乙旅行社表示,若人数不超过20人,每人都按九折收费,超过20人,则超出部分每人按七五折收费,假设组团参加甲、乙两家旅行社两日游的人数均为x人.
(1)请分别写出甲、乙两家旅行社收取组团两日游的总费用y(元)与x(人)之间的函数关系式;
(2)若胡老师组团参加两日游的人数共有32人,请你计算,在甲、乙两家旅行社中,帮助胡老师选择收取总费用较少的一家.
查看答案和解析>>
科目:初中数学 来源: 题型:
某校举行春季运动会,需要在初一年级选取一名志愿者.初一(1)班、初一(2)班、初一(3)班各有2名同学报名参加.现从这6名同学中随机选取一名志愿者,则被选中的这名同学恰好是初一(3)班同学的概率是( )
|
| A. |
| B. |
| C. |
| D. |
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com