
����Ŀ����֪ij��2016����ҵ��ˮ��x���֣������Ӧ����ˮ��y��Ԫ��֮��ĺ�����ϵ��ͼ��
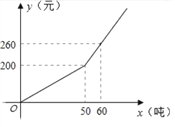
��1����x��50ʱ����y����x�ĺ�����ϵʽ��
��2����ij��ҵ2016��10�·ݵ�ˮ��Ϊ620Ԫ�������ҵ2016��10�·ݵ���ˮ����
��3��Ϊ������ҵ��Լ��ˮ��������2017��1�¿�ʼ������ˮ������80�ֵ���ҵ������ˮ�����ѣ��涨������ҵ����ˮ��x����80�֣������2016���շѱ���ȡˮ���⣬����80�ֵIJ���ÿ��������![]() Ԫ����ˮ�����ѣ���ij��ҵ2017��3�·ݵ�ˮ�Ѻ���ˮ�����ѹ�600Ԫ���������ҵ3�·ݵ���ˮ����
Ԫ����ˮ�����ѣ���ij��ҵ2017��3�·ݵ�ˮ�Ѻ���ˮ�����ѹ�600Ԫ���������ҵ3�·ݵ���ˮ����
���𰸡���1��y=6x��100����2��120�֣���3��100�֣�
����������1����y����x�ĺ�����ϵʽy=kx+b�����루50��200������60��260��������ý���ʽ���ɣ�
��2����y=620���루1����ô𰸼��ɣ�
��3������ˮ��+��ˮ������=600Ԫ���г����̽�����⣬
�⣺��1����y����x�ĺ�����ϵʽy=kx+b��
��ֱ��y=kx+b�����㣨50��200������60��260����
��![]() �����
�����![]() .
.
��y����x�ĺ�����ϵʽ��y=6x��100.
��2����ͼ��֪����y=620ʱ��x��50��
��6x��100=620�����x=120��
�𣺸���ҵ2013��10�·ݵ���ˮ��Ϊ120�֣�
��3��������ã�![]() ��
��
�����x2+40x��14000=0
��ã�x1=100��x2=��140���������⣬��ȥ����
�������ҵ2014��3�·ݵ���ˮ����100�֣�
���㾦�����⿼��һ�κ��������ã�һԪ���η��̺�һԪһ�η��̵����ã�ע���������⣬���ͼ����ʵ��ѡ������ķ������


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������꣬�����Ĺ������г���������д����˼���ķ��㣮ͼ���ǹ������г���ʵ��ͼ��ͼ���ǹ������г��ij���ʾ��ͼ����A��D��C��E��ͬһ��ֱ���ϣ�CD��30cm��DF��20cm��AF��25cm��FD��AE�ڵ�D������CE��15cm���ҡ�EAB��75�㣮
��1����AD�ij���
��2�����E��AB�ľ��룮���ο����ݣ�sin75���0.97��cos75���0.26��tan75���3.73��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ������2��-1��0��2��-1��a������Ϊa�����������ݵ�ƽ����Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ��̣�x-3��(x-2)-p2=0.
��1����֤������pȡ��ֵʱ������������������ȵ�ʵ������
��2���跽����ʵ�����ֱ�Ϊx1��x2��������x12+x22=3 x1x2����ʵ��p��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ͼ��ƽ�������ĸ���A��B��C��D��

��1������������仭ͼ:
�ٻ�����BA��
�ڻ�ֱ��AD��BC�ཻ�ڵ�E��
���ӳ��߶�DC�����߶�DC���ӳ�����ȡһ��F��ʹCF=BC��
������EF��
��2��ͼ����EΪ����Ľ��У�С��ƽ�ǵĽǹ��� ����
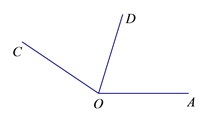
��������֪����AOC=146����ODΪ��AOC��ƽ���ߣ���AOB=90��������ͼ����ͼ��ʾ���벹ȫͼ�Σ������BOD�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����6��x��x�������в���ʽһ���������ǣ�������
A.x��2B.x��3C.x��4D.x��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪ʶ���Խ�����������������̵����⣮�����Ǵ��鱾һ��ϰ�����ֽ���֪ʶ̽����
�����䡿
��ͼ��A��B�Ǻ�l�����������ׯ����Ҫ�ں�l����һ����ˮվC��ʹ����A��B����ׯ�ľ���ĺ���С������ͼ�л�����C��λ�ã���˵�����ɣ�
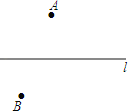
��̽����
��1����ͼ��A��B������ׯ��һ����ֱ����·�����ˣ���ׯ C����·�⣬Ҫ����·�Ͻ�һ������վO��ʹ��AO+BO+CO��С������ͼ�л�����O��λ�ã���˵�����ɣ�

��2����ͼ��A��B��C��D�ĸ���ׯ���ֽ�һ������վO��ʹ��AO+BO+CO+DO��С������ͼ�л�����O��λ�ã���˵�����ɣ�
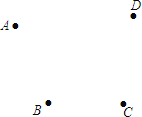
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ABC�У�AB=AC����D��E��F�ֱ�ΪAB��AC��BC�ߵ��е㣮��֤��DE��AF���ഹֱƽ�֣� 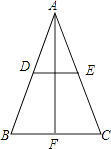
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com