
【题目】已知,如图,△ABC中,AB=AC,点D、E、F分别为AB、AC、BC边的中点.求证:DE与AF互相垂直平分. 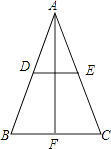
【答案】证明:连接DF,EF, 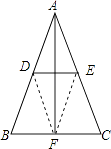
∵点D、E、F分别为AB、AC、BC边的中点,
∴DF=AE= ![]() AC,EF=AD=
AC,EF=AD= ![]() AB,
AB,
∵AB=AC,
∴AD=DF=EF=AE,
∴四边形ADFE是菱形,
∴DE与AF互相垂直平分.
【解析】首先连接DF,EF,由△ABC中,AB=AC,点D、E、F分别为AB、AC、BC边的中点,根据三角形的中位线的性质,易证得AD=DF=EF=AE,继而证得四边形ADFE是菱形,则可证得结论.
【考点精析】掌握线段垂直平分线的性质和等腰三角形的性质是解答本题的根本,需要知道垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;等腰三角形的两个底角相等(简称:等边对等角).


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】已知某市2016年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.
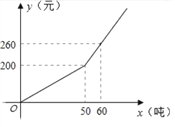
(1)当x≥50时,求y关于x的函数关系式;
(2)若某企业2016年10月份的水费为620元,求该企业2016年10月份的用水量;
(3)为鼓励企业节约用水,该市自2017年1月开始对月用水量超过80吨的企业加收污水处理费,规定:若企业月用水量x超过80吨,则除按2016年收费标准收取水费外,超过80吨的部分每吨另加收![]() 元的污水处理费,若某企业2017年3月份的水费和污水处理费共600元,求这个企业3月份的用水量.
元的污水处理费,若某企业2017年3月份的水费和污水处理费共600元,求这个企业3月份的用水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据要求完成下列题目:
(1)如图中有________块小正方体;
(2) 请在下面方格纸中分别画出它的左视图和俯视图(画出的图都用铅笔涂上阴影);
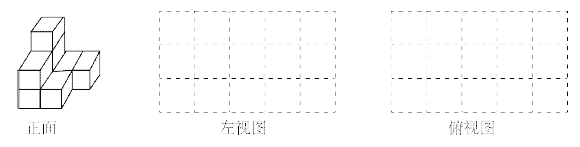
(3)用小正方体搭一个几何体,使得它的俯视图和左视图与你在上图方格中所画的图一致,则这样的几何体最少要________个小正方体,最多要________个小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在频率分布直方图中,以下说法错误的是( )
A.每个小长方形的面积等于频数
B.每个小长方形的面积等于频率
C.频率=频数÷数据总数
D.各个小长方形面积和等于1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次数学测验后,张老师统计了全班50名同学的成绩,其中70分以下的占12%,70﹣80分的占24%,80﹣90分的占36%,请问90分及90分以上的有( )人.
A.13
B.14
C.15
D.28
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一些相同的“○”按如图所示的规律依次摆放,观察每个“龟图”中的“○”的个数,若第n个“龟图”中有245个“○”,则n=( )

A. 14 B. 15 C. 16 D. 17
查看答案和解析>>
科目:初中数学 来源: 题型:
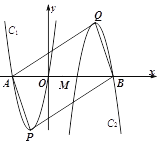
【题目】如图,抛物线![]() 与x轴交于点A,顶点为点P.
与x轴交于点A,顶点为点P.
(1)直接写出抛物线![]() 的对称轴是_______,用含a的代数式表示顶点P的坐标_______;
的对称轴是_______,用含a的代数式表示顶点P的坐标_______;
(2)把抛物线![]() 绕点M(m,0)旋转
绕点M(m,0)旋转![]() 得到抛物线
得到抛物线![]() (其中m>0),抛物线
(其中m>0),抛物线![]() 与x轴右侧的交点为点B,顶点为点Q.
与x轴右侧的交点为点B,顶点为点Q.
①当m=1时,求线段AB的长;
②在①的条件下,是否存在△ABP为等腰三角形,若存在请求出a的值,若不存在,请说明理由;
③当四边形APBQ为矩形时,请求出m与a之间的数量关系,并直接写出当a=3时矩形APBQ的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com