
����Ŀ���ۺ���ʵ��������ת�е���ѧ
���ⱳ������һ���ۺ�ʵ������ϣ�ͬѧ������������Ϊ�����о����ƾ�����ת�е����⣺��֪����ABCD����A��B��C��D�䣬���Ǹ��ԶԽ��ߵĽ����غ��ڵ�O������AA�䣬CC�䣮��������ǽ���������⣺
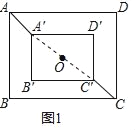
�۲췢�֣���1����ͼ1����A��B���AB����AA����CC���������ϵ��______��
����̽������2����ͼ1�еľ���ABCD���ֲ���������A��B��C��D���Ƶ�O��ʱ����ת�ǶȦ���0�㣼����90�㣩����ͼ2���ھ���A��B��C��D����ת�Ĺ����У���1���еĽ��ۻ�����������������֤����������������˵�����ɣ�
�������㣺��3����ͼ3���ڣ�2���������£�������A��B��C��D���Ƶ�O��ת��AA���A��D��ʱ����AB=6��BC=8��A��B��=3����AA��ij���

���𰸡�AA��=CC��
��������
��1������AC��A��C������������õ���A��A�䡢C�䡢C��ͬһ��ֱ���ϣ����ݾ��ε����ʵõ�OA=OC��OA��=OC�����õ��𰸣�
��2������AC��A��C����֤����A��OA�ա�C��OC������ȫ�������ε�����֤����
��3������AC����C��CE��AB������AB�����ӳ�����E���������ƶ���ε��������B��C�������ݹ��ɶ������㼴�ɣ�
��1��AA��=CC�䣬
�������£�����AC��A��C�䣬
�߾���ABCD����A��B��C��D�䣬��CAB=��C��A��B�䣬
��A��B����AB��
���A��A�䡢C�䡢C��ͬһ��ֱ���ϣ�
�ɾ��ε����ʿ�֪��OA=OC��OA��=OC�䣬
��AA��=CC�䣬
�ʴ�Ϊ��AA��=CC�䣻
��2����1���еĽ��ۻ�������AA��=CC�䣬
�������£�����AC��A��C������AC��A��C����������O��
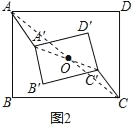
����ת�����ʿ�֪����A��OA=��C��OC��
���ı���ABCD���ı���A��B��C��D�����Ǿ��Σ�
��OA=OC��OA��=OC�䣬
����A��OA����C��OC��
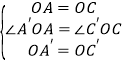 ��
��
���A��OA�ա�C��OC��
��AA��=CC�䣻
��3������AC����C��CE��AB������AB�����ӳ�����E��
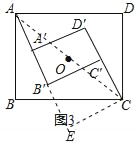
�߾���ABCD����A��B��C��D�䣬
��![]() ����
����![]() ��
��
��ã�B��C��=4��
�ߡ�EB��C=��B��C��C=��E=90�㣬
���ı���B��ECC��Ϊ���Σ�
��EC=B��C��=4��
��Rt��ABC��AC=![]() =10��
=10��
��Rt��AEC��AE=![]() =2
=2![]() ��
��
��AA��+B��E=2![]() ��3����AA��=CC��=B��E��
��3����AA��=CC��=B��E��
��AA��=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
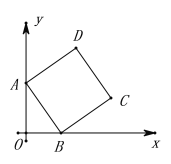
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ACB��90����OC��2BO��AC��6����B������Ϊ��1��0����������y����x2+bx+c����A��B���㣮
��1�����A�����ꣻ
��2���������ߵĽ���ʽ��
��3����P��ֱ��AB�Ϸ��������ϵ�һ�㣬����P��PD��ֱx���ڵ�D�����߶�AB�ڵ�E��ʹPE��![]() DE��
DE��
�����P�����ꣻ
����ֱ��PD���Ƿ���ڵ�M��ʹ��ABMΪֱ�������Σ������ڣ�����������������е�M�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̼���1200Ԫ������һ��T�������к�ܿ����꣬�̼�����2800Ԫ�����˵ڶ�������T�������������ǵ�һ����������2���������۹���5Ԫ��
��1�����̼ҹ����ĵ�һ��T���Ƕ��ټ���
��2��������T������ͬ�ı�����ۣ����ʣ��20���������Ż����������ϣ������T��ȫ������������ʲ�����16%���������������أ�����ôÿ��T���ı�������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����磺��O���O�ϵ�һ��A
��1����������O���ڽ���������ABCDEF���� Ҫ�߹���ͼ����д������������ͼ�ۼ���
��2������CE��BF���ж��ı���BCEF�Ƿ�Ϊ���Σ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij���ξ����һ��̨�ף�����̨������AB��BC�ij���Ϊ6m��AB���ֵ��½ǡ�BADΪ45�㣬BC���ֵ��½ǡ�CBEΪ30�㣬����BD��AD��CE��BE������ΪD��E������Ҫ����̨����Ϊֱ�Ӵ�A��C��̨�ף���������ÿ��̨�ĸ�Ϊ22cm����ô������̨���ж��ٲ㣿�����һ��̨�ĸ߳���15cm�Ҳ���22cmʱ����һ��̨���㣮�����õ������ݣ�![]() ��1.414��
��1.414��![]() ��1.732��
��1.732��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() ���ڵ�
���ڵ�![]() ����
����![]() ����������
Ϊ����������![]() �������������⣺
�������������⣺
��1�����![]() �͵�
�͵�![]() �����ꣻ
�����ꣻ
��2����ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��
��3����ֱ��![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ
��ʹ![]() Ϊ���������Σ������ڣ���ֱ��д����
Ϊ���������Σ������ڣ���ֱ��д����![]() �����ꣻ�������ڣ�˵������.
�����ꣻ�������ڣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���ʵ��
��1�����ⷢ��

��ͼ1��![]() ��
��![]() ��Ϊ�ȱ������Σ���
��Ϊ�ȱ������Σ���![]() ��ͬһֱ���ϣ�����
��ͬһֱ���ϣ�����![]() ����д��
����д��![]() �Ķ������߶�
�Ķ������߶�![]() ֮���������ϵ����˵�����ɣ�
֮���������ϵ����˵�����ɣ�
��2�����̽��
��ͼ2��![]() ��
��![]() ��Ϊ����ֱ�������Σ�
��Ϊ����ֱ�������Σ�![]() ����
����![]() ��ͬһֱ���ϣ�
��ͬһֱ���ϣ�![]() Ϊ
Ϊ![]() ��
��![]() ���ϵĸߣ�����
���ϵĸߣ�����![]() ��
��
��գ���![]() �Ķ���Ϊ____________��
�Ķ���Ϊ____________��
���߶�![]() ֮���������ϵΪ_______________________________��
֮���������ϵΪ_______________________________��
��3����չ����
�ڣ�2���������£���![]() �����ı���
�����ı���![]() �����Ϊ______________��
�����Ϊ______________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƿ���������![]() ��ͼ���һ����֧��
��ͼ���һ����֧��
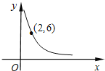
![]() ����ϵ��
����ϵ��![]() ��ֵ��________��
��ֵ��________��
![]() д����ͼ�����һ����֧�ϵ�
д����ͼ�����һ����֧�ϵ�![]() ��������꣺________��________��
��������꣺________��________��
![]() ��
��![]() ��ʲô��Χȡֵʱ��
��ʲô��Χȡֵʱ��![]() ��С��
����![]() ��������
��������
![]() ����Ա���
����Ա���![]() ȡֵ��ΧΪ
ȡֵ��ΧΪ![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������ʶ�Ѿ��������ģ���У����ʦ����![]() Ԫ(ȫ������)����
Ԫ(ȫ������)����![]() ��������Ͱ����֪
��������Ͱ����֪![]() ��Ͱ����
��Ͱ����![]() Ԫ��
Ԫ��![]() ��Ͱ����
��Ͱ����![]() Ԫ���蹺��
Ԫ���蹺��![]() ��Ͱ
��Ͱ![]() ����
����![]() ��Ͱ
��Ͱ![]() ����
����
��1����![]() ����
����![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��2����������![]() ��Ͱ������
��Ͱ������![]() ��Ͱ��
��Ͱ��![]() ����
����
�������ٹ���![]() ��Ͱ���ٸ���
��Ͱ���ٸ���
�ڸ����ٳ�ʵ�ʹ������������ʦ���ܷ��ò��������°�һ����![]() ��Ͱ��������һ��
��Ͱ��������һ��![]() ��Ͱ���ҵ�����
��Ͱ���ҵ�����![]() ��Ͱ������������
��Ͱ������������![]() ��Ͱ����������֪
��Ͱ����������֪![]() ��Ͱ����
��Ͱ����![]() Ԫ���������Ĺ���ʽ��
Ԫ���������Ĺ���ʽ��![]() ��Ͱ������ ����(ֱ��д����)
��Ͱ������ ����(ֱ��д����)
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com