
【题目】如图是某旅游景点的一处台阶,其中台阶坡面AB和BC的长均为6m,AB部分的坡角∠BAD为45°,BC部分的坡角∠CBE为30°,其中BD⊥AD,CE⊥BE,垂足为D,E.现在要将此台阶改造为直接从A至C的台阶,如果改造后每层台阶的高为22cm,那么改造后的台阶有多少层?(最后一个台阶的高超过15cm且不足22cm时,按一个台阶计算.可能用到的数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
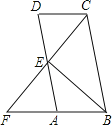
【题目】如图,四边形ABCD中,CD∥AB,E是AD中点,CE交BA延长线于点F.
(1)试说明:CD=AF;
(2)若BC=BF,试说明:BE⊥CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
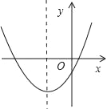
【题目】已知二次函数![]() 的图象如图所示,则下列结论:①ac>0;②a-b+c<0;
的图象如图所示,则下列结论:①ac>0;②a-b+c<0;![]() 当
当![]() 时,
时,![]() ;
;![]() ,其中错误的结论有
,其中错误的结论有![]()
![]()
A. ②③ B. ②④ C. ①③ D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠C=90°,AD平分∠BAC,DE⊥AB于点E,有下列结论:①CD=ED ;②AC+ BE= AB ;③DA平分∠CDE ;④∠BDE =∠BAC;⑤![]() =AB:AC.其中结论正确的个数有()
=AB:AC.其中结论正确的个数有()
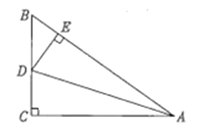
A.5个B.4个
C.3个D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,AC=BC,D为BC中点,CE⊥AD于E,BF∥AC交CE的延长线于F.
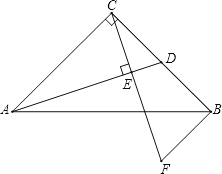
(1)求证:△ACD≌△CBF;
(2)求证:AB垂直平分DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践﹣﹣旋转中的数学
问题背景:在一次综合实践活动课上,同学们以两个矩形为对象,研究相似矩形旋转中的问题:已知矩形ABCD∽矩形A′B′C′D′,它们各自对角线的交点重合于点O,连接AA′,CC′.请你帮他们解决下列问题:
观察发现:(1)如图1,若A′B′∥AB,则AA′与CC′的数量关系是______;
操作探究:(2)将图1中的矩形ABCD保持不动,矩形A′B′C′D′绕点O逆时针旋转角度α(0°<α≤90°),如图2,在矩形A′B′C′D′旋转的过程中,(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由;
操作计算:(3)如图3,在(2)的条件下,当矩形A′B′C′D′绕点O旋转至AA′⊥A′D′时,若AB=6,BC=8,A′B′=3,求AA′的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=mx2+(6﹣2m)x+m﹣3的图象如图所示,则m的取值范围是( )
A. m>3 B. m<3 C. 0≤m≤3 D. 0<m<3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】针对下列图象李明同学说到:图①可能是![]() ;图②可能是
;图②可能是![]() ;图③可能是
;图③可能是![]() ;图④可能是
;图④可能是![]()
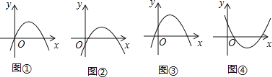
你认为其中必定正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将如图所示的牌面数字分别是1,2,3,4的四张扑克牌背面朝上,洗匀后放在桌面上.
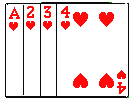
(1)从中随机抽出一张牌,牌面数字是偶数的概率是 ;
(2)从中随机抽出二张牌,两张牌牌面数字的和是5的概率是 ;
(3)先从中随机抽出一张牌,将牌面数字作为十位上的数字,然后将该牌放回并重新洗匀,再随机抽取一张,将牌面数字作为个位上的数字,请用画树状图或列表的方法求组成的两位数恰好是4的倍数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com