
【题目】综合与实践
(1)问题发现

如图1,![]() 和
和![]() 均为等边三角形,点
均为等边三角形,点![]() 在同一直线上,连接
在同一直线上,连接![]() .请写出
.请写出![]() 的度数及线段
的度数及线段![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
(2)类比探究
如图2,![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,点
,点![]() 在同一直线上,
在同一直线上,![]() 为
为![]() 中
中![]() 边上的高,连接
边上的高,连接![]() .
.
填空:①![]() 的度数为____________;
的度数为____________;
②线段![]() 之间的数量关系为_______________________________.
之间的数量关系为_______________________________.
(3)拓展延伸
在(2)的条件下,若![]() ,则四边形
,则四边形![]() 的面积为______________.
的面积为______________.
【答案】(1)![]() ,证明详见解析;(2)①
,证明详见解析;(2)①![]() ;②
;②![]() ;(3)35
;(3)35
【解析】
(1)![]() 和
和![]() 均为等边三角形,根据等边三角形的性质即可证得
均为等边三角形,根据等边三角形的性质即可证得![]() ,所以
,所以![]() 即可求出
即可求出![]() ,证明出
,证明出![]() .
.
(2)①![]() 和
和![]() 均为等腰直角三角形,可证的
均为等腰直角三角形,可证的![]() ,因为
,因为![]() ,所以∠CED=∠CDE=45°,可得出
,所以∠CED=∠CDE=45°,可得出![]() ,②
,②![]() 为
为![]() 中
中![]() 边上的高,则DE=2CM,由全等可知EB=AD,即可得
边上的高,则DE=2CM,由全等可知EB=AD,即可得![]() .
.
(3) 四边形![]() 的面积等于△ACE的面积加上△AEB的面积,根据已知条件利用三角形的面积公式即可求解.
的面积等于△ACE的面积加上△AEB的面积,根据已知条件利用三角形的面积公式即可求解.
(1)结论:![]()
证明:![]() 和
和![]() 均为等边三角形
均为等边三角形
∵![]()
∴![]()
在![]() 和
和![]() 中,
中,
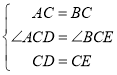
∴![]()
∴![]()
![]()
∴∠![]()
(2)解:∵![]()
∴![]()
∴![]()
在![]() 和
和![]() 中,
中,
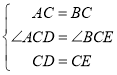
∴![]()
![]()
∵△DCE是等腰直角三角形
∴∠CDE=∠CED=45°
∴![]()
∴![]()
∵![]()
∴EB=AD
∵![]() 为
为![]() 中
中![]() 边上的高
边上的高
∴DE=2CM
∴![]()
(3)∵![]() ,
,![]()
∴AE=10
![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在“美丽沧州,清洁乡村”活动中,高家村村长提出了两种购买垃圾桶方案;方案1:买分类垃圾桶,需要费用3000元,以后每月的垃圾处理费用250元;方案2:买不分类垃圾桶,需要费用1000元,以后每月的垃圾处理费用500元;设方案1的购买费用和每月垃圾处理费用共为![]() 元,交费时间为x个月;方案2的购买费和每月垃圾处理费共为
元,交费时间为x个月;方案2的购买费和每月垃圾处理费共为![]() 元,交费时间为x个月.
元,交费时间为x个月.
(1)直接写出![]() 、
、![]() 与x的函数关系式;
与x的函数关系式;
(2)在同一坐标系内,画出两个函数的图像;
(3)在垃圾桶使用寿命相同的情况下,哪种方案省钱?
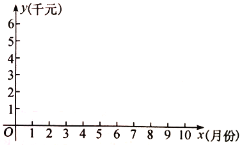
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠C=90°,AD平分∠BAC,DE⊥AB于点E,有下列结论:①CD=ED ;②AC+ BE= AB ;③DA平分∠CDE ;④∠BDE =∠BAC;⑤![]() =AB:AC.其中结论正确的个数有()
=AB:AC.其中结论正确的个数有()
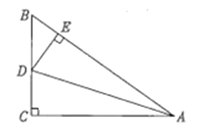
A.5个B.4个
C.3个D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践﹣﹣旋转中的数学
问题背景:在一次综合实践活动课上,同学们以两个矩形为对象,研究相似矩形旋转中的问题:已知矩形ABCD∽矩形A′B′C′D′,它们各自对角线的交点重合于点O,连接AA′,CC′.请你帮他们解决下列问题:
观察发现:(1)如图1,若A′B′∥AB,则AA′与CC′的数量关系是______;
操作探究:(2)将图1中的矩形ABCD保持不动,矩形A′B′C′D′绕点O逆时针旋转角度α(0°<α≤90°),如图2,在矩形A′B′C′D′旋转的过程中,(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由;
操作计算:(3)如图3,在(2)的条件下,当矩形A′B′C′D′绕点O旋转至AA′⊥A′D′时,若AB=6,BC=8,A′B′=3,求AA′的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=mx2+(6﹣2m)x+m﹣3的图象如图所示,则m的取值范围是( )
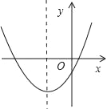
A. m>3 B. m<3 C. 0≤m≤3 D. 0<m<3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】针对下列图象李明同学说到:图①可能是![]() ;图②可能是
;图②可能是![]() ;图③可能是
;图③可能是![]() ;图④可能是
;图④可能是![]()
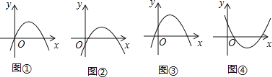
你认为其中必定正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图,点![]() ,
,![]() ,
,![]() 在同一条直线上,连结DC
在同一条直线上,连结DC

(1)请判断![]() 与
与![]() 的位置关系,并证明
的位置关系,并证明
(2)若![]() ,
,![]() ,求
,求![]() 的面积
的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图①,∠QPN的顶点P在正方形ABCD两条对角线的交点处,∠QPN=α,将∠QPN绕点P旋转,旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F(点F与点C,D不重合).
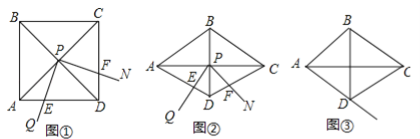
(1)如图①,当α=90°时,DE,DF,AD之间满足的数量关系是 ;
(2)如图②,将图①中的正方形ABCD改为∠ADC=120°的菱形,其他条件不变,当α=60°时,(1)中的结论变为DE+DF=![]() AD,请给出证明;
AD,请给出证明;
(3)在(2)的条件下,若旋转过程中∠QPN的边PQ与射线AD交于点E,其他条件不变,探究在整个运动变化过程中,DE,DF,AD之间满足的数量关系,直接写出结论,不用加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com