
ĄŸÌâÄżĄżŁš12·ÖŁ©ÈçÍŒąÙŁŹĄÏQPN”Ķ„”ăPÔÚŐę·œĐÎABCDÁœÌő¶ÔœÇÏߔĜ»”㎊ŁŹĄÏQPN=ŠÁŁŹœ«ĄÏQPNÈÆ”ăPĐęŚȘŁŹĐęŚȘčęłÌÖĐĄÏQPN”ÄÁœ±ß·Ö±đÓëŐę·œĐÎABCD”ıßADșÍCDœ»ÓÚ”ăEșÍ”ăFŁš”ăFÓë”ăCŁŹDČ»ÖŰșÏŁ©Łź
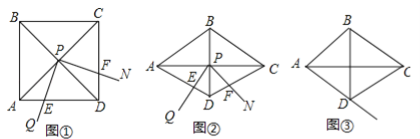
Łš1Ł©ÈçÍŒąÙŁŹ”±ŠÁ=90ĄăʱŁŹDEŁŹDFŁŹADÖźŒäÂúŚă”ÄÊęÁżčŰÏ”ÊÇ Ł»
Łš2Ł©ÈçÍŒąÚŁŹœ«ÍŒąÙÖĐ”ÄŐę·œĐÎABCDžÄÎȘĄÏADC=120Ąă”ÄÁâĐÎŁŹÆäËûÌőŒțČ»±äŁŹ”±ŠÁ=60ĄăʱŁŹŁš1Ł©ÖĐ”ÄœáÂÛ±äÎȘDE+DF=![]() ADŁŹÇëžűłöրÜŁ»
ADŁŹÇëžűłöրÜŁ»
Łš3Ł©ÔÚŁš2Ł©”ÄÌőŒțÏÂŁŹÈôĐęŚȘčęłÌÖĐĄÏQPN”ıßPQÓëÉäÏßADœ»ÓÚ”ăEŁŹÆäËûÌőŒțČ»±äŁŹÌœŸżÔÚŐûžöÔ˶Ż±ä»ŻčęłÌÖĐŁŹDEŁŹDFŁŹADÖźŒäÂúŚă”ÄÊęÁżčŰÏ”ŁŹÖ±œÓĐŽłöœáÂÛŁŹČ»ÓĂŒÓÒÔրÜŁź
ĄŸŽđ°žĄżŁš1Ł©DE+DF=ADŁ»Łš2Ł©ÏêŒûœâÎöŁ»Łš3Ł©ąÙ”±”ăEÂäÔÚADÉÏʱŁŹDE+DF=![]() ADŁŹąÚ”±”ăEÂäÔÚAD”ÄŃÓł€ÏßÉÏʱŁŹDE+DFÖđœ„ÔöŽóŁŹ”±”ăFÓë”ăCÖŰșÏʱDE+DFŚîŽóŁŹŒŽ
ADŁŹąÚ”±”ăEÂäÔÚAD”ÄŃÓł€ÏßÉÏʱŁŹDE+DFÖđœ„ÔöŽóŁŹ”±”ăFÓë”ăCÖŰșÏʱDE+DFŚîŽóŁŹŒŽ![]() ADŁŒDE+DFĄÜ
ADŁŒDE+DFĄÜ![]() ADŁź
ADŁź
ĄŸœâÎöĄż
ÊÔÌ⣚1Ł©žùŸĘŐę·œĐΔÄĐÔÖÊŁŹÒŚÖ€ĄśAPEĄŐĄśDPFŁŹŒŽżÉ”ĂAE=DFŁŹËùÒÔDE+DF=ADŁ»Łš2Ł©ÈĄAD”ÄÖĐ”ăMŁŹÁŹœÓPMŁŹžùŸĘÁâĐΔÄĐÔÖÊŁŹŒŽżÉ”ĂĄśMDPÊǔȱßÈęœÇĐÎŁŹÀûÓĂSASÒŚÖ€ĄśMPEĄŐĄśFPDŁŹÔÙÓÉÈ«”ÈÈęœÇĐΔĶÔÓŠ±ßÏà”ÈżÉ”ĂME=DFŁŹÓÉDE+ME=![]() ADŁŹŒŽżÉ”ĂłöDE+DF=
ADŁŹŒŽżÉ”ĂłöDE+DF=![]() ADŁ»Łš3Ł©ąÙ”±”ăEÂäÔÚADÉÏʱŁŹDE+DF=
ADŁ»Łš3Ł©ąÙ”±”ăEÂäÔÚADÉÏʱŁŹDE+DF=![]() ADŁŹąÚ”±”ăEÂäÔÚAD”ÄŃÓł€ÏßÉÏʱŁŹDE+DFÖđœ„ÔöŽóŁŹ”±”ăFÓë”ăCÖŰșÏʱDE+DFŚîŽóŁŹŒŽ
ADŁŹąÚ”±”ăEÂäÔÚAD”ÄŃÓł€ÏßÉÏʱŁŹDE+DFÖđœ„ÔöŽóŁŹ”±”ăFÓë”ăCÖŰșÏʱDE+DFŚîŽóŁŹŒŽ![]() ADŁŒDE+DFĄÜ
ADŁŒDE+DFĄÜ![]() ADŁź
ADŁź
ÊÔÌâœâÎöŁșœâŁșŁš1Ł©Őę·œĐÎABCD”ĶԜÇÏßACŁŹBDœ»ÓÚ”ăPŁŹ
ĄàPA=PDŁŹĄÏPAE=ĄÏPDF=45ĄăŁŹ
ĄßĄÏAPE+ĄÏEPD=ĄÏDPF+ĄÏEPD=90ĄăŁŹ
ĄàĄÏAPE=ĄÏDPFŁŹ
ÔÚĄśAPEșÍĄśDPFÖĐ
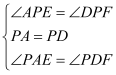
ĄàĄśAPEĄŐĄśDPFŁšASAŁ©ŁŹ
ĄàAE=DFŁŹ
ĄàDE+DF=ADŁ»
Łš2Ł©ÈçÍŒąÚŁŹÈĄAD”ÄÖĐ”ăMŁŹÁŹœÓPMŁŹ
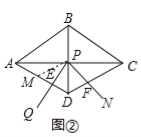
ĄßËıßĐÎABCDÎȘĄÏADC=120Ąă”ÄÁâĐÎŁŹ
ĄàBD=ADŁŹĄÏDAP=30ĄăŁŹĄÏADP=ĄÏCDP=60ĄăŁŹ
ĄàĄśMDPÊǔȱßÈęœÇĐÎŁŹ
ĄàPM=PDŁŹĄÏPME=ĄÏPDF=60ĄăŁŹ
ĄßĄÏPAM=30ĄăŁŹ
ĄàĄÏMPD=60ĄăŁŹ
ĄßĄÏQPN=60ĄăŁŹ
ĄàĄÏMPE=ĄÏFPDŁŹ
ÔÚĄśMPEșÍĄśFPDÖĐŁŹ
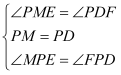
ĄàĄśMPEĄŐĄśFPDŁšASAŁ©
ĄàME=DFŁŹ
ĄàDE+DF=![]() ADŁ»
ADŁ»
Łš3Ł©ÈçÍŒŁŹ
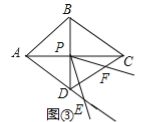
ÔÚŐûžöÔ˶Ż±ä»ŻčęłÌÖĐŁŹ
ąÙ”±”ăEÂäÔÚADÉÏʱŁŹDE+DF=![]() ADŁŹ
ADŁŹ
ąÚ”±”ăEÂäÔÚAD”ÄŃÓł€ÏßÉÏʱŁŹDE+DFÖđœ„ÔöŽóŁŹ”±”ăFÓë”ăCÖŰșÏʱDE+DFŚîŽóŁŹ
ŒŽ![]() ADŁŒDE+DFĄÜ
ADŁŒDE+DFĄÜ![]() ADŁź
ADŁź



| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹ”ăEÊÇÆœĐĐËıßĐÎABCD”ıßBC”ÄÖД㣏ÁŹœÓAEČąŃÓł€œ»DC”ÄŃÓł€ÏßÓÚ”ăF,ÁŹœÓACĄąBF,ĄÏAEC=2ĄÏABCŁ»(1)ÇóÖ€:ËıßĐÎABFCÊÇŸŰĐÎŁ»(2)ÔÚ(1)”ÄÌőŒțÏÂ,ÈôĄśAFDÊǔȱßÈęœÇĐÎ,ÇÒ±ßł€ÎȘ4,ÇóËıßĐÎABFC”ÄĂæ»ęĄŁ

Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÎÒÊĐÄłÏçAĄąBÁœŽćÊąČúžÌéÙŁŹAŽćÓĐžÌéÙ200 ¶ÖŁŹBŽćÓĐžÌéÙ300¶ÖŁźÏÖœ«ŐâĐ©žÌéÙÔË”œCĄąDÁœžöÀäČŰČֿ⣏ÒŃÖȘCČÖżâżÉŽąŽæ240 ¶ÖŁŹDČÖżâżÉŽąŽæ260¶ÖŁ»ŽÓAŽćÔËÍùCĄąDÁœŽŠ”Ä·ŃÓĂ·Ö±đÎȘĂż¶Ö20ÔȘșÍ25ÔȘŁŹŽÓBŽćÔËÍùCĄąDÁœŽŠ”Ä·ŃÓĂ·Ö±đÎȘĂż¶Ö15ÔȘșÍ18ÔȘŁŹÉèŽÓAŽćÔËÍùCČÖżâ”ÄžÌéÙÖŰÁżÎȘx¶ÖŁŹAĄąBÁœŽćÔËÍùÁœČÖżâ”ÄžÌéÙÔËÊä·ŃÓĂ·Ö±đÎȘyAÔȘșÍyBÔȘŁź
(1)ÇółöyAĄąyBÓëxÖźŒä”ÄșŻÊęčŰϔʜŁ»
yA = ________________________ŁŹyB = ________________________Łź
(2)ÊÔÌÖÂÛAĄąBÁœŽćÖĐŁŹÄÄžöŽć”ÄÔË·ŃœÏÉÙŁ»
(3)żŒÂÇ”œBŽć”ÄŸŒĂłĐÊÜÄÜÁŠŁŹBŽć”ÄžÌéÙÔË·ŃČ»”ĂłŹčę4830ÔȘŁźÔÚŐâÖÖÇéżöÏÂŁŹÇëÎÊÔőŃù”śÔËŁŹČĆÄÜÊčÁœŽćÔË·ŃÖźșÍŚîĐĄŁżÇółöŐâžöŚîĐĄÖ”Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒÔÚÒÔ”ăOÎȘÔ”ă”ÄÊęÖáÉÏŁŹ”ăA±íÊŸ”ÄÊęÊÇ3ŁŹ”ăBÔÚÔ”ă”ÄŚóČàŁŹÇÒABŁœ6AO(ÎÒĂÇ°ŃÊęÖáÉÏÁœ”ăÖźŒä”ÄŸàÀëÓñíÊŸÁœ”ă”ÄŽóĐŽŚÖÄžÒ»Æđ±êŒÇŁŹ±ÈÈ磏”ăAÓë”ăBÖźŒä”ÄŸàÀëŒÇŚśAB).
(1)B”ă±íÊŸ”ÄÊęÊÇ_______.
(2)Èô¶Ż”ăPŽÓO”ăłö·ąŁŹÒÔĂżĂë2žö”„λł€¶È”ÄËÙ¶ÈÔÈËÙÏòŚóÔ˶ŻŁŹÎÊŸčęŒžĂëÖÓșóPAŁœ3PBŁżČąÇółöŽËʱP”ăÔÚÊęÖáÉ϶ÔÓŠ”ÄÊę.
(3)Èô¶Ż”ăM.P.N·Ö±đÍŹÊ±ŽÓAĄąOĄąBłö·ąŁŹÔÈËÙÏòÓÒÔ˶ŻŁŹÆäËٶȷֱđÎȘ1žö”„λł€¶È/Ăë.2žö”„λł€¶È/Ăë.4žö”„λł€¶È/Ă룏ÉèÔ˶ŻÊ±ŒäÎȘtĂ룏ÇëÖ±œÓĐŽłöPM.PN.MNÖĐÈÎÒâÁœžöÏà”Èʱ”ÄʱŒä.
![]()
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
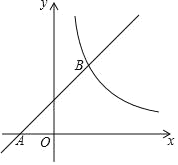
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚÆœĂæÖ±œÇŚű±êÏ”xOyÖĐŁŹÒ»ŽÎșŻÊęyŁœx+b”ÄÍŒÏóŸčę”ăAŁš©2ŁŹ0Ł©ŁŹÓë·Ž±ÈÀęșŻÊęyŁœ![]() ŁšxŁŸ0Ł©”ÄÍŒÏóœ»ÓÚBŁšaŁŹ4Ł©Łź
ŁšxŁŸ0Ł©”ÄÍŒÏóœ»ÓÚBŁšaŁŹ4Ł©Łź
Łš1Ł©ÇóÒ»ŽÎșŻÊęșÍ·Ž±ÈÀęșŻÊę”ıíŽïÊœŁ»
Łš2Ł©ÉèMŁšm©2ŁŹmŁ©ÊÇÖ±ÏßABÉÏÒ»”㣏čęMŚśMNĄÎxÖᣏœ»·Ž±ÈÀęșŻÊęyŁœ![]() ŁšxŁŸ0Ł©”ÄÍŒÏóÓÚ”ăNŁŹÈôAONMÎȘ¶„”ă”ÄËıßĐÎÎȘÆœĐĐËıßĐÎŁŹÇó”ăM”ÄŚű±êŁź
ŁšxŁŸ0Ł©”ÄÍŒÏóÓÚ”ăNŁŹÈôAONMÎȘ¶„”ă”ÄËıßĐÎÎȘÆœĐĐËıßĐÎŁŹÇó”ăM”ÄŚű±êŁź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁșÔÚÊęÖáÉÏ![]() ”ă±íÊŸÊę
”ă±íÊŸÊę![]() ŁŹ
ŁŹ![]() ”ă±íÊŸÊę
”ă±íÊŸÊę![]() ŁŹ
ŁŹ![]() ”ă±íÊŸÊę
”ă±íÊŸÊę![]() ŁŹ
ŁŹ![]() ÊÇŚîŽó”ÄžșŐûÊ꣏ÇÒ
ÊÇŚîŽó”ÄžșŐûÊ꣏ÇÒ![]() Ąą
Ąą![]() ÂúŚă
ÂúŚă![]() Óë
Óë![]() »„ÎȘÏà·ŽÊę.
»„ÎȘÏà·ŽÊę.
![]()
(1)![]() ______ŁŹ
______ŁŹ![]() ______ŁŹ
______ŁŹ![]() ______.
______.
(2)Èôœ«ÊęÖáŐÛ”țŁŹÊč”Ă![]() ”ăÓë
”ăÓë![]() ”ăÖŰșÏŁŹÔò”ă
”ăÖŰșÏŁŹÔò”ă![]() ÓëÊę______±íÊŸ”Ä”ăÖŰșÏŁ»
ÓëÊę______±íÊŸ”Ä”ăÖŰșÏŁ»
(3)”ă![]() Ąą
Ąą![]() Ąą
Ąą![]() żȘÊŒÔÚÊęÖáÉÏÔ˶ŻŁŹÈô”ă
żȘÊŒÔÚÊęÖáÉÏÔ˶ŻŁŹÈô”ă![]() ÒÔĂżĂë2žö”„λł€¶È”ÄËÙ¶ÈÏòŚóÔ˶ŻŁŹÍŹÊ±ŁŹ”ă
ÒÔĂżĂë2žö”„λł€¶È”ÄËÙ¶ÈÏòŚóÔ˶ŻŁŹÍŹÊ±ŁŹ”ă![]() șÍ”ă
șÍ”ă![]() ·Ö±đÒÔĂżĂë1žö”„λł€¶ÈșÍ3žö”„λł€¶È”ÄËÙ¶ÈÏòÓÒÔ˶ŻŁŹŒÙÉè
·Ö±đÒÔĂżĂë1žö”„λł€¶ÈșÍ3žö”„λł€¶È”ÄËÙ¶ÈÏòÓÒÔ˶ŻŁŹŒÙÉè![]() ĂëÖÓčęșóŁŹÈô”ă
ĂëÖÓčęșóŁŹÈô”ă![]() Óë”ă
Óë”ă![]() ÖźŒä”ÄŸàÀë±íÊŸÎȘ
ÖźŒä”ÄŸàÀë±íÊŸÎȘ![]() ŁŹ”ă
ŁŹ”ă![]() Óë”ă
Óë”ă![]() ÖźŒä”ÄŸàÀë±íÊŸÎȘ
ÖźŒä”ÄŸàÀë±íÊŸÎȘ![]() .
.
ąÙÇëÎÊŁș![]() ”ÄÖ”ÊÇ·ńËæŚĆʱŒä
”ÄÖ”ÊÇ·ńËæŚĆʱŒä![]() ±ä»Ż¶űžÄ±äŁżÈô±ä»ŻŁŹË”ĂśÀíÓÉŁ»ÈôČ»±äŁŹÇëÇóÆäÖ”.
±ä»Ż¶űžÄ±äŁżÈô±ä»ŻŁŹË”ĂśÀíÓÉŁ»ÈôČ»±äŁŹÇëÇóÆäÖ”.
ąÚÌœŸżŁșÔÚ(3)”ÄÇéżöÏÂŁŹÈô”ă![]() Ąą
Ąą![]() ÏòÓÒÔ˶ŻŁŹ”ă
ÏòÓÒÔ˶ŻŁŹ”ă![]() ÏòŚóÔ˶ŻŁŹËٶȱŁłÖČ»±äŁŹ
ÏòŚóÔ˶ŻŁŹËٶȱŁłÖČ»±äŁŹ![]() Ö”ÊÇ·ńËæŚĆʱŒä
Ö”ÊÇ·ńËæŚĆʱŒä![]() ”ı仯¶űžÄ±äŁŹÈô±ä»ŻŁŹÇë˔ÜÀíÓÉŁ»ÈôČ»±äŁŹÇëÇóÆäÖ”.
”ı仯¶űžÄ±äŁŹÈô±ä»ŻŁŹÇë˔ÜÀíÓÉŁ»ÈôČ»±äŁŹÇëÇóÆäÖ”.
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄż2008Äê6ÔÂ1ÈŐÆđŁŹÎÒčúʔʩĄ°ÏȚËÜÁŁŹżȘÊŒÓĐł„ÊčÓĂ»·±ŁčșÎïŽüŁźÎȘÁËÂúŚăÊĐłĄĐèÇóŁŹÄłł§ŒÒÉúČú![]() ÁœÖÖżîÊœ”ÄČŒÖÊ»·±ŁčșÎïŽüŁŹĂżÌìčČÉúČú4500žöŁŹÁœÖÖčșÎïŽü”ijɱŸșÍÊÛŒÛÈçÏÂ±íŁŹÉèĂżÌìÉúČú
ÁœÖÖżîÊœ”ÄČŒÖÊ»·±ŁčșÎïŽüŁŹĂżÌìčČÉúČú4500žöŁŹÁœÖÖčșÎïŽü”ijɱŸșÍÊÛŒÛÈçÏÂ±íŁŹÉèĂżÌìÉúČú![]() ÖÖčșÎïŽü
ÖÖčșÎïŽü![]() žöŁŹĂżÌìčČ»ńÀû
žöŁŹĂżÌìčČ»ńÀû![]() ÔȘŁź
ÔȘŁź
łÉ±ŸŁšÔȘ/žöŁ© | ÊÛŒÛŁšÔȘ/žöŁ© | |
| 2 | 2.3 |
| 3 | 3.5 |
Łš1Ł©Çółö![]() čŰÓÚ
čŰÓÚ![]() ”ÄșŻÊęœâÎöÊœŁ»
”ÄșŻÊęœâÎöÊœŁ»
Łš2Ł©ÈçčûžĂł§ĂżÌìŚî¶àͶÈëłÉ±Ÿ10000ÔȘŁŹÄÇĂŽĂżÌìŚî¶à»ńÀû¶àÉÙÔȘŁż
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÎȘÓœÓ4ÔÂ23ÈŐ”ÄÊÀœç¶ÁÊéÈŐŁŹÄłÊé”êÖƶšÁ˻ŒÆ»źŁŹÈç±íÊǻŒÆ»ź”ÄČż·ÖĐĆÏąŁș
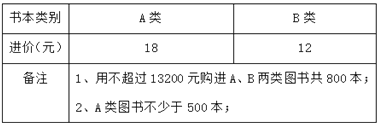
(1)ŃîŸÀíČ鿎ŒÆ»źÊ±·ąÏÖŁșAÀàÍŒÊé”ıêŒÛÊÇBÀàÍŒÊé±êŒÛ”Ä1.5±¶.ÈôčËżÍÓĂ540ÔȘčșÂòÍŒÊ飏ÄÜ”„¶ÀčșÂòAÀàÍŒÊé”ÄÊęÁżÇĄșĂ±È”„¶ÀčșÂòBÀàÍŒÊé”ÄÊęÁżÉÙ10±Ÿ.ÇëÇółöAĄąBÁœÀàÍŒÊé”ıêŒÛ.
(2)ŸÊĐłĄ”śČéșóŁŹŃîŸÀí·ąÏÖËûĂÇžßčÀÁËĄ°¶ÁÊéÈŐĄ±¶ÔÍŒÊéÏúÊÛ”ÄÓ°ÏìŁŹ±ă”śŐûÁËÏúÊÛ·œ°žŁșAÀàÍŒÊéĂż±Ÿ°Ž±êŒÛœ””ÍaÔȘ(![]() )ÏúÊÛŁŹBÀàÍŒÊéŒÛžńČ»±ä.ÄÇĂŽÊé”êÓŠÈçșÎœű»őČĆÄÜ»ń”ĂŚîŽóÀûÈó.
)ÏúÊÛŁŹBÀàÍŒÊéŒÛžńČ»±ä.ÄÇĂŽÊé”êÓŠÈçșÎœű»őČĆÄÜ»ń”ĂŚîŽóÀûÈó.
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚŸŰĐÎABCDÖĐŁŹAB=4cmŁŹAD=12cmŁŹ”ăPÔÚAD±ßÉÏÒÔĂżĂë1cm”ÄËٶȎӔăAÏò”ăDÔ˶ŻŁŹ”ăQÔÚBC±ßÉÏŁŹÒÔĂżĂë4cm”ÄËٶȎӔăCłö·ąŁŹÔÚCBŒäÍù·”Ô˶ŻŁŹÁœžö”ăÍŹÊ±łö·ąŁŹ”±”ăP”œŽï”ăDÊ±ÍŁÖčŁšÍŹÊ±”ăQÒČÍŁÖ裩ŁŹÔÚŐâ¶ÎʱŒäÄÚŁŹÏ߶ÎPQÓĐŁšĄĄŁ©ŽÎÆœĐĐÓÚABŁż
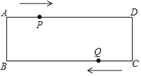
A. 1 B. 2 C. 3 D. 4
Č鿎Žđ°žșÍœâÎö>>
čúŒÊѧУÓĆŃĄ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com