
【题目】2008年6月1日起,我国实施“限塑令”,开始有偿使用环保购物袋.为了满足市场需求,某厂家生产![]() 两种款式的布质环保购物袋,每天共生产4500个,两种购物袋的成本和售价如下表,设每天生产
两种款式的布质环保购物袋,每天共生产4500个,两种购物袋的成本和售价如下表,设每天生产![]() 种购物袋
种购物袋![]() 个,每天共获利
个,每天共获利![]() 元.
元.
成本(元/个) | 售价(元/个) | |
| 2 | 2.3 |
| 3 | 3.5 |
(1)求出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)如果该厂每天最多投入成本10000元,那么每天最多获利多少元?
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
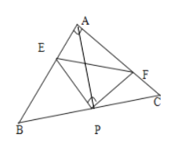
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角三角形EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,给出以下五个结论:①AE=CF;②∠APE=∠CPF;③△EPF是等腰直角三角形;④EF=AP;⑤![]() ,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合)上述结论正确的是_____________.(填序号)
,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合)上述结论正确的是_____________.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )

A. 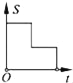 B.
B. 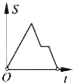 C.
C. 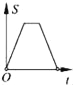 D.
D. 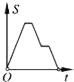
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图①,∠QPN的顶点P在正方形ABCD两条对角线的交点处,∠QPN=α,将∠QPN绕点P旋转,旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F(点F与点C,D不重合).
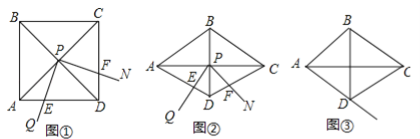
(1)如图①,当α=90°时,DE,DF,AD之间满足的数量关系是 ;
(2)如图②,将图①中的正方形ABCD改为∠ADC=120°的菱形,其他条件不变,当α=60°时,(1)中的结论变为DE+DF=![]() AD,请给出证明;
AD,请给出证明;
(3)在(2)的条件下,若旋转过程中∠QPN的边PQ与射线AD交于点E,其他条件不变,探究在整个运动变化过程中,DE,DF,AD之间满足的数量关系,直接写出结论,不用加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天快递配送员张强一直在一条南北走向的街道上送快递,如果规定向北为正,向南为负,这天他从出发点开始所走的路程(单位:![]() )记录如下:
)记录如下:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)这天送完最后一个快递时,张强在出发点的什么方向?距离出发点有多远?
(2)如果张强送完快递时,需立刻返回出发点,那么他这天送快递(含返回)共耗油多少升(每千米耗油![]() )?
)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶.已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示,当乙到达终点A时,甲还需( )分钟到达终点B.
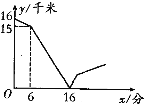
A. 78B. 76C. 16D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
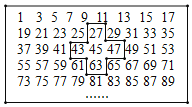
【题目】如图,将连续的奇数1,3,5,7……排成如下的数表,用十字形框框出5个数.
探究规律一:设十字框中间的奇数为x,则框中五个奇数的和用含x的整式表示为 ,这说明被十字框框中的五个奇数的和一定是正整数n(n>1)的倍数,这个正整数n是 ;
探究规律二:落在十字框中间且位于第二列的一组奇数是21,39,57,75,…,则这一组数可以用整式表示为18m+3(m为序数),同样,落在十字框中间且位于第三列的一组奇数可以表示为 ;(用含m的式子表示)
运用规律:
(1)已知被十字框框中的五个奇数的和为2025,则十字框中间的奇数是 ,这个奇数落在从左往右第 列;
(2)被十字框框中的五个奇数的和可能是2020吗?若能,请求出这五个数:若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】建立模型:
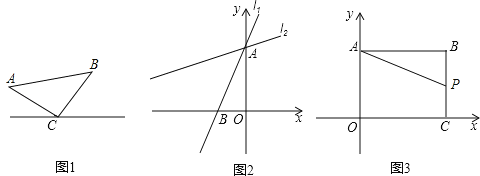
如图1,已知△ABC,AC=BC,∠C=90°,顶点C在直线l上.
操作:
过点A作AD⊥l于点D,过点B作BE⊥l于点E.求证:△CAD≌△BCE.
模型应用:
(1)如图2,在直角坐标系中,直线l1:y=![]() x+4与y轴交于点A,与x轴交于点B,将直线l1绕着点A顺时针旋转45°得到l2.求l2的函数表达式.
x+4与y轴交于点A,与x轴交于点B,将直线l1绕着点A顺时针旋转45°得到l2.求l2的函数表达式.
(2)如图3,在直角坐标系中,点B(8,6),作BA⊥y轴于点A,作BC⊥x轴于点C,P是线段BC上的一个动点,点Q(a,2a﹣6)位于第一象限内.问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形,若能,请求出此时a的值,若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com