
【题目】建立模型:
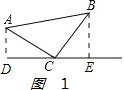
如图1,已知△ABC,AC=BC,∠C=90°,顶点C在直线l上.
操作:
过点A作AD⊥l于点D,过点B作BE⊥l于点E.求证:△CAD≌△BCE.
模型应用:
(1)如图2,在直角坐标系中,直线l1:y=![]() x+4与y轴交于点A,与x轴交于点B,将直线l1绕着点A顺时针旋转45°得到l2.求l2的函数表达式.
x+4与y轴交于点A,与x轴交于点B,将直线l1绕着点A顺时针旋转45°得到l2.求l2的函数表达式.
(2)如图3,在直角坐标系中,点B(8,6),作BA⊥y轴于点A,作BC⊥x轴于点C,P是线段BC上的一个动点,点Q(a,2a﹣6)位于第一象限内.问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形,若能,请求出此时a的值,若不能,请说明理由.
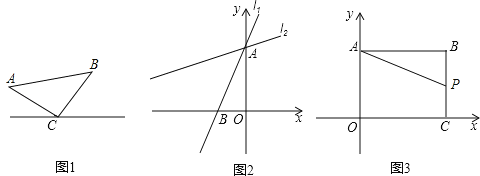
【答案】(1)y=![]() x+4;(2)a的值为
x+4;(2)a的值为![]() 或4.
或4.
【解析】
试题分析:操作:根据余角的性质,可得∠ACD=∠CBE,根据全等三角形的判定,可得答案;
应用(1)根据自变量与函数值的对应关系,可得A、B点坐标,根据全等三角形的判定与性质,可得CD,BD的长,根据待定系数法,可得AC的解析式;
(2)根据全等三角形的性质,可得关于a的方程,根据解方程,可得答案.
解:操作:如图1:
 ,
,
∵∠ACD+∠BCE=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠CBE.
在△ACD和△CBE中,
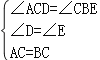
∴△CAD≌△BCE(AAS);
(1)∵直线y=![]() x+4与y轴交于点A,与x轴交于点B,
x+4与y轴交于点A,与x轴交于点B,
∴A(0,4)、B(﹣3,0).
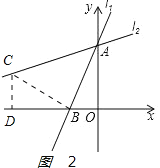
如图2:
 ,
,
过点B做BC⊥AB交直线l2于点C,过点C作CD⊥x轴
在△BDC和△AOB中,
 ,
,
△BDC≌△AOB(AAS),
∴CD=BO=3,BD=AO=4.OD=OB+BD=3+4=7,
∴C点坐标为(﹣7,3).
设l2的解析式为y=kx+b,将A,C点坐标代入,得
![]() ,
,
解得![]()
l2的函数表达式为y=![]() x+4;
x+4;
(2)由题意可知,点Q是直线y=2x﹣6上一点.
如图3:
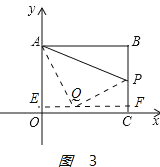 ,
,
过点Q作EF⊥y轴,分别交y轴和直线BC于点E、F.
在△AQE和△QPF中,
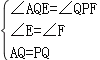 ,
,
∴△AQE≌△QPF(AAS),
AE=QF,即6﹣(2a﹣6)=8﹣a,
解得a=4
如图4:
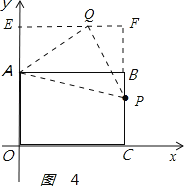 ,
,
过点Q作EF⊥y轴,分别交y轴和直线BC于点E、F,
AE=2a﹣12,FQ=8﹣a.
在△AQE和△QPF中,
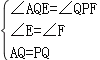 ,
,
△AQE≌△QPF(AAS),
AE=QF,即2a﹣12=8﹣a,
解得a=![]() ;
;
综上所述:A、P、Q可以构成以点Q为直角顶点的等腰直角三角形,a的值为![]() 或4.
或4.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】仔细阅读下面例题,然后按要求解答问题:
例题:已知二次三项式 ![]() 有一个因式是
有一个因式是 ![]() ,求另一个因式以及
,求另一个因式以及 ![]() 的值.
的值.
解法一:设另一个因式为 ![]() ,
,
得 ![]() ,
,
则 ![]() ,
,
![]() ,
,
解得 ![]() ,
,
![]() 另一个因式为
另一个因式为 ![]() ,
,![]() 的值为
的值为 ![]() .
.
解法二:∵二次三项式 x2-4x+m 有一个因式是 (x+3),
∴当x+3=0,即x=-3时,x2-4x+m=0.
把x=-3代入x2-4x+m=0,
得m=-21,
而x2-4x-21=(x+3)(x-7).
问题:分别仿照以上两种方法解答下面问题:
(1)已知二次三项式 ![]() 有一个因式是
有一个因式是 ![]() ,求另一个因式以及
,求另一个因式以及 ![]() 的值.
的值.
解法一: 解法二:
(2)直接回答:
已知关于x的多项式 2x3![]() (3
(3![]() k)x2
k)x2![]() 2x
2x![]() 1有一个因式是
1有一个因式是 ![]() 1,则k的值为_________.
1,则k的值为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+3|+(b﹣2)2=0.
(1)求A、B两点的对应的数a、b;
(2)点C在数轴上对应的数为x,且x是方程2x+1=![]() x﹣8的解.
x﹣8的解.
①求线段BC的长;
②在数轴上是否存在点P,使PA+PB=BC?求出点P对应的数;若不存在,说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某居民小区的一块宽为2a米,长为b米的长方形空地,为了美化环境,准备在这块长方形空地的四个顶点处修建一个半径为a米的扇形花台,然后在花台内种花,其余种草.
(1)请分别用含a、b的式子表示种花和种草的面积.(答案保留π)
(2)如果建造花台及种花费用每平方米需要资金100元,种草每平方米需要资金50元,那么美化这块空地共需资金多少元?(答案保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2011年5月20日是第22个中国学生营养日,某校社会实践小组在这天开展活动,调查快餐营养情况.他们从食品安全监督部门获取了一份快餐的信息(如图).根据信息,解答下列问题. 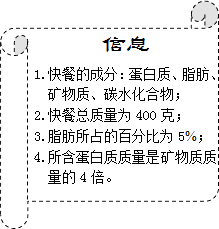
(1)求这份快餐中所含脂肪质量;
(2)若碳水化合物占快餐总质量的40%,求这份快餐所含蛋白质的质量;
(3)若这份快餐中蛋白质和碳水化合物所占百分比的和不高于85%,求其中所含碳水化合物质量的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形草坪ABCD中,∠B=90°,AB=24m,BC=7m,CD=15m,AD=20m.
(1)判断∠ADC是否是直角,并说明理由;
(2)试求四边形草坪ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别延长ABCD的边BA、DC到点E、H,使得AE=AB,CH=CD,连接EH,分别交AD、BC于点F、G. 求证:△AEF≌△CHG.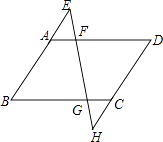
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些有用的式子,或可以求出一些不规则图形的面积.

(1)如图1,是将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的方法计算这个图形的面积,你能发现什么结论,请写出来.
(2)如图2,是将两个边长分别为a和b的正方形拼在一起,B、C、G三点在同一直线上,连接BD和BF,若两正方形的边长满足a+b=10,ab=20,你能求出阴影部分的面积吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com