练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，四边形草坪ABCD中，∠B=90°，AB=24m，BC=7m，CD=15m，AD=20m.

    （1）判断∠ADC是否是直角，并说明理由；

    （2）试求四边形草坪ABCD的面积.

    【答案】（1）∠D是直角，理由见解析；（2）234m2．

    【解析】

    （1）连接AC，先根据勾股定理求出AC的长，再求出AD的长，结合勾股定理的逆定理得到∠D是直角；

    （2）由S四边形ABCD=S△ABC+S△ADC即可得出结论．

    （1）∠D是直角，理由如下：

    连接AC，

    ∵∠B=90°，AB=24m，BC=7m，

    ∴AC2=AB2+BC2=242+72=625，

    ∴AC=25（m）．

    又∵CD=15m，AD=20m，152+202=252，即AD2+DC2=AC2，

    ∴△ACD是直角三角形，或∠D是直角；

    （2）S四边形ABCD=S△ABC+S△ADC

    =234（m2）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

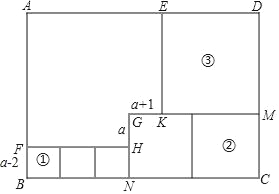
    【题目】如图所示，用三种大小不等的正方形①②③和…个缺角的正方形拼成一个长方形ABCD（不重叠且没有缝隙），若GH＝a，GK＝a+1，BF＝a﹣2

    （1）试用含a的代数式表示：正方形②的边长CM的长＝　 　，正方形③的边长DM的长＝　 　；

    （2）求长方形ABCD的周长（用含a的代数式表示）；并求出当a＝3时，长方形周长的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我国汉代数学家赵爽为了证明勾股定理，创制了一副“弦图”，后人称其为“赵爽弦图”（如图1）．图2由弦图变化得到，它是由八个全等的直角三角形拼接而成．记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1 ， S2 ， S3 ， 若S1+S2+S3=10，则S2的值是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】光明中学有两块边长为x米的正方形空地，现设想按两种方式种植草皮，方式一：如图①，在正方形空地上留两条宽为2m米的路，其余种植草皮；方式二：如图②，在正方形空地四周各留一块边长为m米的正方形空地植树，其余种植草皮．学校准备两种方式都用5000元购进草皮．

    (1)写出按图①，②两种方式购买草皮的单价；

    (2)当x＝14，m＝2时，求按两种方式购买草皮的单价各是多少(结果均保留整数)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

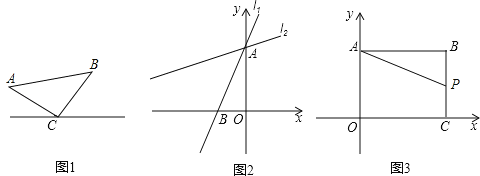
    【题目】建立模型：

    如图1，已知△ABC，AC=BC，∠C=90°，顶点C在直线l上．

    操作：

    过点A作AD⊥l于点D，过点B作BE⊥l于点E．求证：△CAD≌△BCE．

    模型应用：

    （1）如图2，在直角坐标系中，直线l1：y=x+4与y轴交于点A，与x轴交于点B，将直线l1绕着点A顺时针旋转45°得到l2．求l2的函数表达式．

    （2）如图3，在直角坐标系中，点B（8，6），作BA⊥y轴于点A，作BC⊥x轴于点C，P是线段BC上的一个动点，点Q（a，2a﹣6）位于第一象限内．问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形，若能，请求出此时a的值，若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小聪和小明沿同一条笔直的马路同时从学校出发到某图书馆查阅资料，学校与 图书馆的路程是 千米，小聪骑自行车，小明步行，当小聪从原路回到学校时，小明刚好到 达图书馆，图中折线 和线段 分别表示两人离学校的路程 （千米）与所经过的 时间 （分钟）之间的函数关系，请根据图像回答下列问题：

    （1）小聪在图书馆查阅资料的时间为 分钟；小聪返回学校的速度为 千米/分钟．

    （2）请你求出小明离开学校的路程 （千米）与所经过的时间 （分钟）之间的函数表达式；

    （3）若设两人在路上相距不超过 千米时称为可以“互相望见”，则小聪和小明可以“互相 望见”的时间共有多少分钟？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，把矩形纸片ABCD沿EF折叠后，使得点D与点B重合，点C落在点C′的位置上．

    （1）△BEF是等腰三角形吗？试说明理由；

    （2）若AB＝4，AD＝8，求CF的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一条排水管的截面如图所示．已知排水管的截面圆半径OB=10，截面圆圆心O到水面的距离OC是6，则水面宽AB是（ ）
    A.16
    B.10
    C.8
    D.6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市积极开展“阳光体育进校园”活动，各校学生坚持每天锻炼一小时，某校根据实际，决定主要开设A：乒乓球，B：篮球，C：跑步，D：跳绳四种运动项目，为了解学生最喜欢哪一种项目，随机抽取了部分学生进行调查，并将调查结果绘制成如下统计图．请你结合图中信息解答下列问题．

    （1）请计算最喜欢B项目的人数所占的百分比．

    （2）请计算D项所在扇形图中的圆心角的度数．

    （3）请把统计图补充完整．

    查看答案和解析>>

    同步练习册答案