
【题目】光明中学有两块边长为x米的正方形空地,现设想按两种方式种植草皮,方式一:如图①,在正方形空地上留两条宽为2m米的路,其余种植草皮;方式二:如图②,在正方形空地四周各留一块边长为m米的正方形空地植树,其余种植草皮.学校准备两种方式都用5000元购进草皮.

(1)写出按图①,②两种方式购买草皮的单价;
(2)当x=14,m=2时,求按两种方式购买草皮的单价各是多少(结果均保留整数).
科目:初中数学 来源: 题型:
【题目】观察算式:
![]() ;
;![]() ;
;![]() ;
;![]() ;……
;……
(1)请根据你发现的规律填空:7×9+1=________2;
(2)用含n的等式表示上面的规律:________;
(3)用找到的规律解决下面的问题:计算:
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)先化简,再求值:(2+a)(2﹣a)+a(a﹣5b)+3a5b3÷(﹣a2b)2,其中ab=﹣![]() .
.
(2)若x2+4x﹣4=0,求3(x﹣2)2﹣6(x+1)(x﹣1)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程在招标时,接到甲、乙两个工程队的投标书.施工一天,需付甲工程队工程款1.2万元,乙工程队工程款0.5万元.工程领导小组根据甲、乙两队的投标书测算,有以下方案:
方案(1):甲队单独完成这项工程刚好如期完成.
方案(2):乙队单独完成这项工程要比规定的日期多用6天.
方案(3):若甲、乙两队合做3天,余下的工程由乙队单独做也正好如期完成.
试问:在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某居民小区的一块宽为2a米,长为b米的长方形空地,为了美化环境,准备在这块长方形空地的四个顶点处修建一个半径为a米的扇形花台,然后在花台内种花,其余种草.
(1)请分别用含a、b的式子表示种花和种草的面积.(答案保留π)
(2)如果建造花台及种花费用每平方米需要资金100元,种草每平方米需要资金50元,那么美化这块空地共需资金多少元?(答案保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在梯形ABCD中,AD∥BC,∠ABC=90°,对角线AC、BD相交于点O.下列条件中,不能判断对角线互相垂直的是( ) 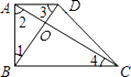
A.∠1=∠4
B.∠1=∠3
C.∠2=∠3
D.OB2+OC2=BC2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形草坪ABCD中,∠B=90°,AB=24m,BC=7m,CD=15m,AD=20m.
(1)判断∠ADC是否是直角,并说明理由;
(2)试求四边形草坪ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l1:y=﹣![]() x+3与坐标轴分别交于点A,B,与直线l2:y=x交于点C.
x+3与坐标轴分别交于点A,B,与直线l2:y=x交于点C.
(1)求A,B两点的坐标;
(2)求△BOC的面积;
(3)如图2,若有一条垂直于x轴的直线l以每秒1个单位的速度从点A出发沿射线AO方向作匀速滑动,分别交直线l1,l2及x轴于点M,N和Q.设运动时间为t(s),连接CQ.
①当OA=3MN时,求t的值;
②试探究在坐标平面内是否存在点P,使得以O、Q、C、P为顶点的四边形构成菱形?若存在,请直接写出t的值;若不存在,请说明理由.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣ ![]() (x﹣1)2+3与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.
(x﹣1)2+3与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.
(1)如图1.求点A的坐标及线段OC的长;
(2)点P在抛物线上,直线PQ∥BC交x轴于点Q,连接BQ.
①若含45°角的直角三角板如图2所示放置.其中,一个顶点与点C重合,直角顶点D在BQ上,另一个顶点E在PQ上.求直线BQ的函数解析式;
②若含30°角的直角三角板一个顶点与点C重合,直角顶点D在直线BQ上,另一个顶点E在PQ上,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com