
【题目】我市某乡A、B两村盛产柑橘,A村有柑橘200 吨,B村有柑橘300吨.现将这些柑橘运到C、D两个冷藏仓库,已知C仓库可储存240 吨,D仓库可储存260吨;从A村运往C、D两处的费用分别为每吨20元和25元,从B村运往C、D两处的费用分别为每吨15元和18元,设从A村运往C仓库的柑橘重量为x吨,A、B两村运往两仓库的柑橘运输费用分别为yA元和yB元.
(1)求出yA、yB与x之间的函数关系式;
yA = ________________________,yB = ________________________.
(2)试讨论A、B两村中,哪个村的运费较少;
(3)考虑到B村的经济承受能力,B村的柑橘运费不得超过4830元.在这种情况下,请问怎样调运,才能使两村运费之和最小?求出这个最小值.
【答案】(1)yA=5000-5x,yB=3x+4680 (2)当x=40,两村的运费一样多;当0≤x<40时,B村的费用较少;当40<x≤200时,A村的费用较少.(3)从A村运往C仓库的柑桔重量为50吨,运往D仓库的柑桔重量为150吨,从B村运往C仓库的柑桔重量为190吨,运往D仓库的柑桔重量为110吨才能使两村所花运费之和最小,最少总运费是9580元.
【解析】
(1)由A村共有柑橘200吨,从A村运往C仓库x吨,剩下的运往D仓库,故运往D仓库为(200-x)吨,由A村已经运往C仓库x吨,C仓库可储存240吨,故B村应往C仓库运(240-x)吨,剩下的运往D仓库,剩下的为300-(240-x),即可得到B村运往D仓库的吨数, 再由从A村运往C、D两厂的费用分别为每吨20元和25元,从B村运往C、D两厂的费用分别为每吨15元和18元,即可分别求得yA、yB与x之间的函数关系式;
(2)分yA=yB、yA>yB、yA<yB三种情况进行解答即可;
(3)首先由B村的柑桔运费不得超过4830元得出不等式,求出自变量的取值范围,求出两个函数和,根据自变量的取值范围,利用一次函数的性质求得最值.
(1)根据题意得:yA=20x+25(200-x)=5000-5x,
yB=15(240-x)+18![]() =3x+4680,
=3x+4680,
x的取值范围是:0≤x≤200,
故答案为: yA=5000-5x,yB=3x+4680
(2)①当yA=yB,即5000-5x=3x+4680,解得x=40,
当x=40,两村的运费一样多,
②当yA>yB,即5000-5x>3x+4680,解得x<40,
当0≤x<40时,B村的费用较少,
③当yA<yB,即5000-5x<3x+4680,解得x>40,
当40<x≤200时,A村的费用较少.
(3)由yB≤4830,得3x+4680≤4830,解得x≤50,
设A、B两村运费之和为y,
则y=yA+yB=5000-5x+3x+4680=-2x+9680,
∵-2<0,
∴y随着x的增大而减小,
又0≤x≤50,
∴当x=50时,y有最小值,最小值是y=-2×50+9680=9580(元),
200-50=150,240-50=190,60+50=110.
∴若B村的柑桔运费不得超过4830元,在这种情况下,从A村运往C仓库的柑桔重量为50吨,运往D仓库的柑桔重量为150吨,从B村运往C仓库的柑桔重量为190吨,运往D仓库的柑桔重量为110吨才能使两村所花运费之和最小,最少总运费是9580元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,这是网上盛传的一个关于数学的诡辩问题截图,表1是它的示意表.我们一起来解答“为什么多出了2元".

花去 | 剩余 | |
买牛肉 | 40元 | 60元 |
买猪脚 | 30元 | 30元 |
买蔬菜 | 18元 | 12元 |
买调料 | 12元 | 0元 |
总计 | 100元 | 102元 |
表1
花去 | 剩余 | |
买牛肉 | 40元 | 60元 |
买猪脚 | 30元 | 30元 |
买蔬菜 | 元 | 元 |
买调料 | 元 | 0元 |
总计 | 100元 | 103元 |
表2
花去 | 剩余 | |
买物品1 | a元 | x元 |
买物品2 | b元 | y元 |
买物品3 | c元 | z元 |
买物品4 | d元 | 0元 |
总计 | 100元 | w元 |
表3
花去 | 剩余 | |
买牛肉 | 元 | 元 |
买猪脚 | 元 | 元 |
买蔬菜 | 元 | 元 |
买调料 | 元 | 元 |
总计 | 元 | / |
表4
(1)为了解释“剩余金额总计”与“我手里有100元"无关,请按要求填写表2中的空格.
(2)如表3中,直接写出各代数式的值: .
①a+b+c+d=_ ;
②a+x=__ ;
③a+b+y=_ ;
④a+b+c+z=_ 。
(3)如表3中,a、b、c、d都是正整数,则w的最大值等于_ ,最小值等于_ ,由此可以知道“为什么多出了2元”只是一个诡辩而已.
(4)我们将“花去”记为“一”,“剩余”记为“+”,请在表4中将表1数据重新填写.
查看答案和解析>>
科目:初中数学 来源: 题型:
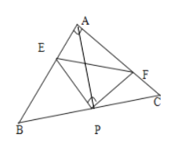
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角三角形EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,给出以下五个结论:①AE=CF;②∠APE=∠CPF;③△EPF是等腰直角三角形;④EF=AP;⑤![]() ,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合)上述结论正确的是_____________.(填序号)
,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合)上述结论正确的是_____________.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
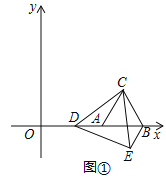
【题目】如图①,在平面直角坐标系中,等边△ABC的顶点A,B的坐标分别为(5,0),(9,0),点D是x轴正半轴上一个动点,连接CD,将△ACD绕点C逆时针旋转60°得到△BCE,连接DE.
(Ⅰ)直接写出点C的坐标,并判断△CDE的形状,说明理由;
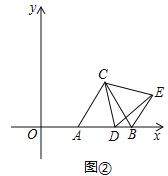
(Ⅱ)如图②,当点D在线段AB上运动时,△BDE的周长是否存在最小值?若存在,求出△BDE的最小周长及此时点D的坐标;若不存在,说明理由;
(Ⅲ)当△BDE是直角三角形时,求点D的坐标.(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天上午,一出租车司机始终在一条南北走向的笔直马路上营运,(出发点记作为点O,约定向南为正,向北为负),期间一共运载6名乘客,行车里程(单位:千米)依先后次序记录如下:﹢7,﹣3,﹢6,﹣1,﹢2,﹣4.
(1)出租车在行驶过程中,离出发点O最远的距离是______千米;
(2)将最后一名乘客送到目的地,出租车离出发点O多远?在O点的什么方向?
(3)出租车收费标准为:起步价(不超过3千米)为8元,超过3千米的部分每千米的价格为1.5元,求司机这天上午的营业额.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国移动公司开设适合普通用户的两种通讯业务分别是:“全球通”用户先缴![]() 元月租,然后每分钟通话费用
元月租,然后每分钟通话费用![]() 元;“神州行”用户不用缴纳月租费,每分钟通话
元;“神州行”用户不用缴纳月租费,每分钟通话![]() 元.(通话均指拨打本地电话)
元.(通话均指拨打本地电话)
![]() 设一个月内通话时间约为
设一个月内通话时间约为![]() 分钟(
分钟(![]() 且
且![]() 为整数),求这两种用户每月需缴的费用分别是多少元?(用含
为整数),求这两种用户每月需缴的费用分别是多少元?(用含![]() 的式子表示)
的式子表示)
![]() 若张老师一个月通话约
若张老师一个月通话约![]() 分钟,请你给他提个建议,应选择哪种移动通讯方式合算一些?并说明理由.
分钟,请你给他提个建议,应选择哪种移动通讯方式合算一些?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )

A. 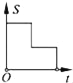 B.
B. 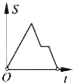 C.
C. 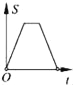 D.
D. 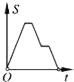
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图①,∠QPN的顶点P在正方形ABCD两条对角线的交点处,∠QPN=α,将∠QPN绕点P旋转,旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F(点F与点C,D不重合).
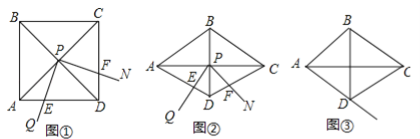
(1)如图①,当α=90°时,DE,DF,AD之间满足的数量关系是 ;
(2)如图②,将图①中的正方形ABCD改为∠ADC=120°的菱形,其他条件不变,当α=60°时,(1)中的结论变为DE+DF=![]() AD,请给出证明;
AD,请给出证明;
(3)在(2)的条件下,若旋转过程中∠QPN的边PQ与射线AD交于点E,其他条件不变,探究在整个运动变化过程中,DE,DF,AD之间满足的数量关系,直接写出结论,不用加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com