
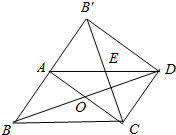
 如图所示,在平行四边形ABCD纸片中,AC与BD相交于点O,将△ABC沿对角线AC翻折得到△AB′C且点B、A、B'处于同一直线上,
如图所示,在平行四边形ABCD纸片中,AC与BD相交于点O,将△ABC沿对角线AC翻折得到△AB′C且点B、A、B'处于同一直线上,分析 (1)根据平行四边形的性质以及已知条件求证出四边形ACDB′是平行四边形,进而求出四边形ACDB′是矩形;
(2)根据矩形的性质以及平行四边形的性质求出△ACD的面积,因为△AEC和△EDC可以看作是等底等高的三角形,所以S△AEC=$\frac{1}{2}$S△ACD=3cm2.
解答 (1)证明:∵四边形ABCD是平行四边形.
∴AB平行且等于CD.
∵△AB′C是由△ABC翻折得到的,AB⊥AC,
∴AB=AB′,点A、B、B′在同一条直线上.
∴AB′∥CD,
∴四边形ACDB′是平行四边形.
∵B′C=BC=AD.
∴四边形ACDB′是矩形.
(2)解:由四边形ACDB′是矩形,得AE=DE.
∵S?ABCD=12cm2,
∴S△ACD=6cm2,
∴S△AEC=$\frac{1}{2}$S△ACD=3cm2.
点评 本题主要考查的是平行四边形的性质、矩形的判定、三角形面积公式,明确△AEC和△EDC可以看作是等底等高的三角形是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
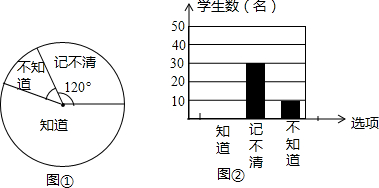
| A. | 440人 | B. | 495人 | C. | 550人 | D. | 6人 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -22÷(-2)2=1 | B. | ${({-2\frac{1}{3}})^3}=-8\frac{1}{27}$ | C. | $-5÷\frac{1}{3}×\frac{3}{5}=-25$ | D. | -32+(-3)2=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AB=BC=5,AC=6,过点A作AD∥BC,点P、Q分别是射线AD、线段BA上的动点(不与A、B重合),且AP=BQ,过点P作PE∥AC交线段AQ于点O,连接PQ,设△POQ面积为y,AP=x.
如图,△ABC中,AB=BC=5,AC=6,过点A作AD∥BC,点P、Q分别是射线AD、线段BA上的动点(不与A、B重合),且AP=BQ,过点P作PE∥AC交线段AQ于点O,连接PQ,设△POQ面积为y,AP=x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com