
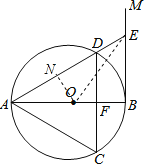
【题目】如图,![]() 是
是![]() 的直径,过点
的直径,过点![]() 作
作![]() 的切线
的切线![]() ,弦
,弦![]() ,交
,交![]() 于点
于点![]() ,且弧
,且弧![]() 弧
弧![]() ,连接
,连接![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .
.

(1)求证:![]() 是等边三角形;
是等边三角形;
(2)若![]() ,求
,求![]() 的半径.
的半径.
【答案】(1)见解析;(2)2![]() .
.
【解析】
(1)由AB是⊙O的直径,BM是⊙O的切线,得到AB⊥BE,由于CD∥BE,得到CD⊥AB,根据垂径定理得到弧![]() 弧
弧![]() ,于是得到弧
,于是得到弧![]() 弧
弧![]() =弧AC ,问题即可得证;
=弧AC ,问题即可得证;
(2)连接OE,过O作ON⊥AD于N,由(1)知,△ACD是等边三角形,得到∠DAC=60°又直角三角形的性质得到BE=![]() AE,ON=
AE,ON=![]() AO,设⊙O的半径为:r则ON=
AO,设⊙O的半径为:r则ON=![]() r,AN=DN=
r,AN=DN=![]() r,由于得到EN=2+
r,由于得到EN=2+![]() r,BE=
r,BE=![]() AE=
AE=![]() ,在Rt△DEF与Rt△BEO中,由勾股定理列方程即可得到结论.
,在Rt△DEF与Rt△BEO中,由勾股定理列方程即可得到结论.
(1)证明:∵AB是⊙O的直径,BM是⊙O的切线,
∴AB⊥BE,
∵CD∥BE,
∴CD⊥AB,
∴弧AD=弧AC,
∵弧![]() 弧
弧![]() ,
,
∴弧![]() 弧
弧![]() =弧AC,
=弧AC,
∴AD=AC=CD,
∴△ACD是等边三角形;
(2)解:连接OE,过O作ON⊥AD于N,由(1)知,△ACD是等边三角形,
∴∠DAC=60°
∵AD=AC,CD⊥AB,
∴∠DAB=30°,
∴BE=![]() AE,ON=
AE,ON=![]() AO,
AO,
设⊙O的半径为:r,
∴ON=![]() r,AN=DN=
r,AN=DN=![]() r,
r,
∴EN=2+![]() r,BE=
r,BE=![]() AE=
AE=![]() ,
,
在Rt△NEO与Rt△BEO中,
OE2=ON2+NE2=OB2+BE2,
即(![]() )2+(2+
)2+(2+![]() )2=r2+(
)2=r2+(![]() )2,
)2,
∴r=2![]() ,
,
∴OE2=(![]() )2+25=28,
)2+25=28,
∴OE=2![]() .
.


科目:初中数学 来源: 题型:
【题目】学校为表彰在“了不起我的国”演讲比赛中获奖的选手,决定购买甲、乙两种图书作为奖品.已知购买30本甲种图书,50本乙种图书共需1350元;购买50本甲种图书,30本乙种图书共需1450元.
(1)求甲、乙两种图书的单价分别是多少元?
(2)学校要求购买甲、乙两种图书共40本,且甲种图书的数量不少于乙种图书数量的![]() ,请设计最省钱的购书方案.
,请设计最省钱的购书方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校小伟同学酷爱健身,一天去爬山锻炼,在出发点C处测得山顶部A的仰角为30度,在爬山过程中,每一段平路(CD、EF、GH)与水平线平行,每一段上坡路(DE、FG、HA)与水平线的夹角都是45度,在山的另一边有一点B(B、C、D同一水平线上),斜坡AB的坡度为2:1,且AB长为900![]() ,其中小伟走平路的速度为65.7米/分,走上坡路的速度为42.3米/分.则小伟从C出发到坡顶A的时间为( )(图中所有点在同一平面内
,其中小伟走平路的速度为65.7米/分,走上坡路的速度为42.3米/分.则小伟从C出发到坡顶A的时间为( )(图中所有点在同一平面内![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
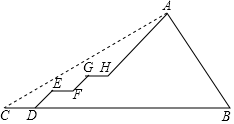
A.60分钟B.70分钟C.80分钟D.90分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.

(1)求证:BG=DE;
(2)若E为AD中点,FH=2,求菱形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高铁站已于几年前投入使用,计划在广场内种植![]() 两种花木共10500棵,若
两种花木共10500棵,若![]() 花木数量比
花木数量比![]() 花木数量的一半多1500棵.
花木数量的一半多1500棵.
(1)![]() 两种花木的数量分别是多少棵?
两种花木的数量分别是多少棵?
(2)如果园林处安排27人同时种植这两种花木,每人每天能种植![]() 花木50棵或
花木50棵或![]() 花木30棵,应分别安排多少人种植
花木30棵,应分别安排多少人种植![]() 花木和
花木和![]() 花木,才能确保同时完成各自的任务?
花木,才能确保同时完成各自的任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,已知:在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() 分别在
分别在![]() 上,连接
上,连接![]() ,点
,点![]() 为线段
为线段![]() 的中点,连接
的中点,连接![]() ,则线段
,则线段![]() 与
与![]() 之间的数量关系是 ,位置关系是
之间的数量关系是 ,位置关系是

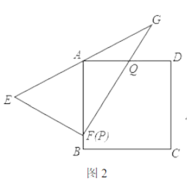
(2)如图2所示,已知:正方形![]() 将
将![]() 斜边
斜边![]() 的中点与点
的中点与点![]() 重合,直角顶点
重合,直角顶点![]() 落在正方形的
落在正方形的![]() 边上,
边上,![]() 的两直角边分别交
的两直角边分别交![]() 边于
边于![]() 两点(点
两点(点![]() 与点
与点![]() 重合),求证:
重合),求证:![]() ;
;
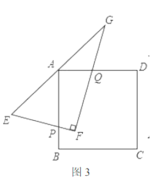
(3)如图3,若将![]() 绕着点
绕着点![]() 逆时针旋转
逆时针旋转![]() ,两直角边分别交
,两直角边分别交![]() 边于
边于![]() 两点,如图3所示:判断四条线段
两点,如图3所示:判断四条线段![]() 之间是否存在什么确定的相等关系?若存在,证明你的结论.若不存在,请说明理由.
之间是否存在什么确定的相等关系?若存在,证明你的结论.若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知绿茶每千克成本50元,经研究发现销量y(kg)随销售单价x(元/kg)的变化而变化,具体变化规律如表所示:
销售单价x(元/kg) | … | 70 | 75 | 80 | 85 | 90 | … |
月销售量y(kg) | … | 100 | 90 | 80 | 70 | 60 | … |
(1)请根据上表,写出y与x之间的函数关系式(不必写出自变量x的取值范围);
(2)若该绿茶的月销售利润为w(元),且售单价得高于80元,求w与x之间的函数关系式,并求出x为何值时,w的值最大?
(3)已知商家经销一种绿茶,用于装修门面已投资3000元,在第一个月,按使w获得最大值的销售单价进行销售后;在第二个月受物价部门干预,销售单价不得高于78元,要想在全部收回装修投资的基础上使这两个月的总利润至少达到1722元,求第二个月的销售单价的取值范围?
查看答案和解析>>
科目:初中数学 来源: 题型:
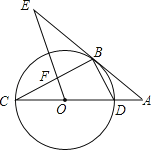
【题目】如图,CD是⊙O的直径,点B在⊙O上,连接BC、BD,直线AB与CD的延长线相交于点A,AB2=ADAC,OE∥BD交直线AB于点E,OE与BC相交于点F.
(1)求证:直线AE是⊙O的切线;
(2)若⊙O的半径为3,cosA=![]() ,求OF的长.
,求OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校以随机抽样的方式开展了中学生喜欢数学的程度的问卷调查,调查的结果分为A(不喜欢)、B(一般)、C(比较喜欢)、D(非常喜欢)四个等级,图1、图2是根据采集的数据绘制的两幅不完整的统计图.
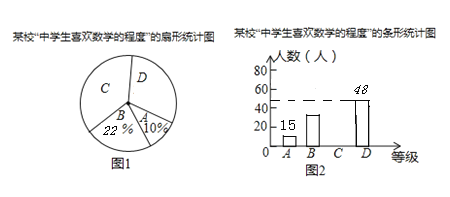
(1)本次抽样调查的样本容量是;
(2)请直接在图2中补全C对应的条形统计图;
(3)若该校有学生1000人,请根据调查结果,估计“比较喜欢”的学生人数为多少人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com