
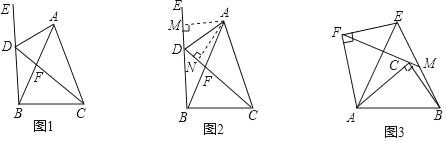
����Ŀ���Ķ����ϣ�С����������һ�����⣺��ͼ1������ABC�У�AB��AC������B������BE����DΪ����BE�ϵĵ㣬����AD��CD���ҡ�BDC����BAC����֤��ADƽ�֡�CDE��С������۲�ͼ�Σ��ַ���һ����ȵĽǣ�������ȵ�һ�ԽǺ�һ�Աߣ�����A��˫��ֱ������ȫ�������Σ���ͼ2���Ӷ�����������
��1�������Ķ����ϣ�֤��ADƽ�֡�CDE��
��ѧ����֪ʶ��ο�С���ķ����������������⣺
��2����ͼ3����Rt��ABC�У���ACB��90������A��������Rt��ABC�Ƶ�A��ʱ����ת�õ���AEF����C�Ķ�Ӧ��Ϊ��F��������BE��FC���ӳ�FC��B�ڵ�M��
���ҳ�ͼ�����BCM��ȵĽǣ�������֤����
�ڲ����߶�CF��BM֮���������ϵ���ú�����ʽ�ӱ�ʾ������֤����IJ��룮
���𰸡���1������������2���١�BCM����EFM�����ɼ��������ڲ��룺FC��2BMcos�������ɼ�������
��������
��1����ͼ2�У���AM��BE��M��AN��CD��N������ȫ�������ε�����֤��AM��AN���ɣ�
��2���ٽ��ۣ���BCM����EFM�����õȽǵ�������֤�����ɣ��ڲ��룺FC��2BMcos������ͼ3�У�����AM����AE��FM�ڵ�O������֤��AM��BE�����������������ε����ʼ���֤����
��1��֤������ͼ2�У���AM��BE��M��AN��CD��N��
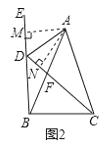
�ߡ�BDF����CAF����DFB����AFC��
���DBF����ACF��
�ߡ�AMB����ANC��90������ABM����ACN��AB��AC��
���ABM�ա�ACN��AAS����
��AM��AN����AM��DM��AN��DN��
��ADƽ�֡�CDE��
��2���⣺�ٽ��ۣ���BCM����EFM��
���ɣ���ͼ3�У���AC��AF��
���ACF����AFC��
�ߡ�ACB����AFE��90����
���ACF+��BCM��90������AFC+��MFE��90����
���BCM����EFM��
�۲��룺FC��2BMcos����
���ɣ���ͼ3�У�����AM����AE��FM�ڵ�O��
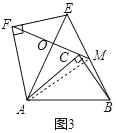
�ߡ�CAB����EAF������
���BAE����CAF��
��AC��AF��AE��AB��
���AFC����ACF����AEB����ABE��
�ߡ�AOF����MOE��
���AOF�ס�MOE��
��![]() ��
��
��![]() ���ߡ�EOF����AOM��
���ߡ�EOF����AOM��
���EOF�ס�MOA��
���OAM����EFO��
�ߡ�OFO���ϡ�OEM����OFA+��EFO��90����
���OAM+��OEM��90����
���AME��90����
��AE��AB��
��BM��![]() BE��
BE��
�ߡ�FAC�ס�EAB��
��![]() ��cos����
��cos����
��![]() ��cos����
��cos����
��FC��2BMcos����


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ���������������еĸ��
���������������еĸ��![]() ��
��![]() ��
��![]() ��
��![]() ��������������еĸ�㼰�̶ȵ�ֱ�߷ֱ���ͼ1��ͼ2��ͼ3�л���һ��������������������
��������������еĸ�㼰�̶ȵ�ֱ�߷ֱ���ͼ1��ͼ2��ͼ3�л���һ��������������������![]() ��
��

��1������![]() ��
��![]() ���Ҳ����
���Ҳ����![]() ��
��![]() ��
��![]() ��
��![]() �غϣ�
�غϣ�
��2��![]() ��ͼ1��ͼ2��ͼ3�е�����ֵ�ֱ�Ϊ1��
��ͼ1��ͼ2��ͼ3�е�����ֵ�ֱ�Ϊ1��![]() ��2.
��2.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ijУ���꼶����1000���ܵ�ˮƽ�����������ȡ�����������в��ԣ����Ѳ��Գɼ���ΪD��C��B��A�ĸ��ȴλ��Ƴ���ͼ��ʾ�IJ�������ͳ��ͼ��������ͼ����������⣺
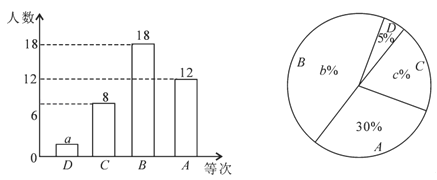
��1��a=�� ����b=�� ����c=�� ����
��2������ͳ��ͼ�б�ʾC�ȴε��������Ե�Բ�ĽǵĶ���Ϊ�� ���ȣ�
��3��ѧУ������A�ȴεļס��ҡ����������������У����ѡȡ���������μ�ȫ����ѧ��1000���ܱ����������б�������״ͼ������ס�����������ͬʱ��ѡ�еĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ij��ѧѧ�����������������ϲ���������顢������������ӡ����ʵ���ĸ�������������е���ͳ�ƣ��ִӸ�У�����ȡ![]() ��ѧ����Ϊ�����������ʾ�����ķ����ռ����ݣ������ʾ������ÿ��ѧ��ֻ��ѡ������һ��������ݵ���õ������ݻ��Ƴ�����ͼ��ʾ��������������ͳ��ͼ����ͼ���ṩ����Ϣ������������⣺
��ѧ����Ϊ�����������ʾ�����ķ����ռ����ݣ������ʾ������ÿ��ѧ��ֻ��ѡ������һ��������ݵ���õ������ݻ��Ƴ�����ͼ��ʾ��������������ͳ��ͼ����ͼ���ṩ����Ϣ������������⣺
��1����n��ֵ��
��2������Уѧ������1200�ˣ��Թ��Ƹ�Уϲ�������ӵ�ѧ��������
��3�������鵽ϲ���������4��ѧ������3��������1��Ů�����ִ���4��ѧ���������ȡ2��ѧ������ǡ�ó鵽2�������ĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��ax2+bx+c��a��0��������y���Ա���x�IJ��ֶ�Ӧֵ���±���
x | ���� | ��1 | 0 | 1 | 4 | ���� |
y | ���� | 12 | 6 | 2 | 2 | ���� |
��1������κ����Ľ���ʽ��
��2��ֱ��д������ʽax2+bx+c��2��0�Ľ⼯���� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ɽijũ����Ϊ��ץס����һ��С���ٵ��̻�����������A��B���ּ���Ʒ��������A�ּ���Ʒ4����B�ּ���Ʒ3������Ҫ550Ԫ��������A�ּ���Ʒ8����B�ּ���Ʒ5������Ҫ1050Ԫ��
��1����A��B���ּ���Ʒÿ���������Ԫ��
��2������ũ���־������������ּ���Ʒ��100���������г�������ʽ���ת�����ڹ�����100������Ʒ���ʽ�����7500Ԫ����������7650Ԫ����ô��ũ���ֹ��м��ֽ���������
��3��������ÿ��A�ּ���Ʒ�ɻ�����30Ԫ��ÿ��B�ּ���Ʒ�ɻ�����20Ԫ���ڵڣ�2���ʵĸ��ֽ��������У���һ�ַ������������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڼס������������IJ������״���װ��3����ȫ��ͬ��С�����ֱ��������0��1��2���Ҵ���װ��3����ȫ��ͬ��С�����ֱ����������1����2��0���ִӼ״��������ȡһ��С������¼���е�����Ϊx���ٴ��Ҵ��������ȡһ��С������¼���е�����Ϊy��ȷ����M����Ϊ��x��y����
��1������״ͼ���б����оٵ�M���п��ܵ����ꣻ
��2�����M��x��y���ں���y=-x+1��ͼ���ϵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���������a2>b2����ôa>b����![]() ������ƽ������4���۹�һ������ֻ��һ��ֱ������ֱ֪��ƽ�У��ܹ���x�ķ���
������ƽ������4���۹�һ������ֻ��һ��ֱ������ֱ֪��ƽ�У��ܹ���x�ķ���![]() û��ʵ����,��ôm��ȡֵ��Χ��m>1��m��0����ȷ����( )
û��ʵ����,��ôm��ȡֵ��Χ��m>1��m��0����ȷ����( )
A. 0��B. 1��C. 2��D. 3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��l1��x���ڵ㣨1��0����ֱ��l2��x���ڵ㣨2��0����ֱ��l3��x���ڵ㣨3��0��������ֱ��ln��x���ڵ㣨n��0��������y��x��ͼ����ֱ��l1��l2��l3������ln�ֱ��ڵ�A1��A2��A3������An������y��2x��ͼ����ֱ��l1��l2��l3������ln�ֱ��ڵ�B1��B2��B3������Bn�������OA1B1���������S1���ı���A1A2B2B1���������S2���ı���A2A3B3B2���������S3�������ı���An��1AnBnBn��1���������Sn����ôS2018����������
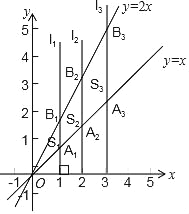
A. 2017.5B. 2018C. 2018.5D. 2019
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com