练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，AB为⊙O的直径，直线l与⊙O相切于点C，AD⊥l，垂足为D，AD交⊙O于点E，连接OC、BE．若AE=6，OA=5，则线段DC的长为 ．

    【答案】4
    【解析】解：OC交BE于F，如图，∵AB为⊙O的直径，
    ∴∠AEB=90°，
    ∵AD⊥l，
    ∴BE∥CD，
    ∵CD为切线，
    ∴OC⊥CD，
    ∴OC⊥BE，
    ∴四边形CDEF为矩形，
    ∴CD=EF，
    在Rt△ABE中，BE= = =8，
    ∵OF⊥BE，
    ∴BF=EF=4，
    ∴CD=4．
    故答案为4．

    OC交BE于F，如图，有圆周角定理得到∠AEB=90°，加上AD⊥l，则可判断BE∥CD，再利用切线的性质得OC⊥CD，则OC⊥BE，原式可判断四边形CDEF为矩形，所以CD=EF，接着利用勾股定理计算出BE，然后利用垂径定理得到EF的长，从而得到CD的长．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中的点P和图形M，给出如下的定义：若在图形M上存在一点Q，使得P、Q两点间的距离小于或等于1，则称P为图形M的关联点．
    （1）当⊙O的半径为2时，
    ①在点P1（ ，0），P2（ ， ），P3（ ，0）中，⊙O的关联点是 ．
    ②点P在直线y=﹣x上，若P为⊙O的关联点，求点P的横坐标的取值范围．
    （2）⊙C的圆心在x轴上，半径为2，直线y=﹣x+1与x轴、y轴交于点A、B．若线段AB上的所有点都是⊙C的关联点，直接写出圆心C的横坐标的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=﹣（a+b）x2﹣2cx+a﹣b中，a、b、c是△ABC的三边．
    （1）当抛物线与x轴只有一个交点时，判断△ABC是什么形状；
    （2）当x=﹣ 时，该函数有最大值 ，判断△ABC是什么形状．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数y=ax2+bx+c，自变量x与函数y的对应值如表：

    x

    …

    ﹣5

    ﹣4

    ﹣3

    ﹣2

    ﹣1

    0

    …

    y

    …

    4

    0

    ﹣2

    ﹣2

    0

    4

    …

    下列说法正确的是（ ）
    A.抛物线的开口向下
    B.当x＞﹣3时，y随x的增大而增大
    C.二次函数的最小值是﹣2
    D.抛物线的对称轴是x=﹣

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，⊙C过原点，且与两坐标轴分别交于点A、点B，点A的坐标为（0，3），M是第三象限内 上一点，∠BMO=120°，则⊙C的半径长为（ ）

    A.6
    B.5
    C.3
    D.3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明是个爱动脑筋的孩子，他在学完与圆有关的角圆周角、圆心角后，意犹未尽，又查阅到了与圆有关的另一种角﹣﹣﹣﹣﹣﹣弦切角．请同学们先仔细阅读下面的材料，再完成后面的问题．
    材料：顶点在圆上，一边与圆相交，另一边与圆相切的角叫做弦切角．如图1，弧 是弦切角∠PAB所夹的弧，他发现弦切角与它所夹的弧所对的圆周角有关系．

    问题1：如图2，直线DB切⊙O于点A，∠PCA是圆周角，当圆心O位于边AC上时，
    求证：∠PAD=∠PCA，请你写出这个证明过程．
    问题拓展：
    如果圆心O不在∠PCA的边上，∠PAD=∠PCA还成立吗？如图3，当圆心O在∠PCA的内部时，小明证明了这个结论是成立的．他的思路是：作直线AE，联结PE，由问题1的结论可知∠PAD=∠PEA，而∠PCA=∠PEA，从而证明∠PAD=∠PC．
    问题2：如图4，当圆心O在∠PCA的外部时，∠PAD=∠PCA仍然成立．请你仿照小明的思路证明这个结论．
    运用：如图5，AD是△ABC中∠BAC的平分线，经过点A的⊙O与BC切于点D，与AB、AC分别相交于E、F．求证：EF∥BC．（提示：可以直接使用本题中的结论）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的一元二次方程x2+（4m+1）x+2m﹣1=0；
    （1）求证：不论m 任何实数，方程总有两个不相等的实数根；
    （2）若方程的两根为x1、x2且满足 ，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是二次函数y=ax2+bx+c图象的一部分，且过点A （3，0），二次函数图象的对称轴是x=1．下列结论：①b2＞4ac；②ac＞0； ③a﹣b+c＞0； ④4a+2b+c＜0．其中错误的结论有（ ）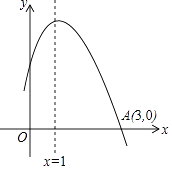

    A.1个
    B.2个
    C.3个
    D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，抛物线y=ax2+ +c经过原点O和A（4，2），与x轴交于点C，点M、N同时从原点O出发，点M以2个单位/秒的速度沿y轴正方向运动，点N以1个单位/秒的速度沿x轴正方向运动，当其中一个点停止运动时，另一点也随之停止．

    （1）求抛物线的解析式和点C的坐标；
    （2）在点M、N运动过程中，
    ①若线段MN与OA交于点G，试判断MN与OA的位置关系，并说明理由；
    ②若线段MN与抛物线相交于点P，探索：是否存在某一时刻t，使得以O、P、A、C为顶点的四边形是等腰梯形？若存在，请求出t值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案