
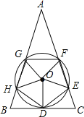
【题目】如图,五边形![]() 是边长为
是边长为![]() 的正五边形,
的正五边形,![]() 是正五边形
是正五边形![]() 的外接圆,过点
的外接圆,过点![]() 作
作![]() 的切线,与
的切线,与![]() 、
、![]() 的延长线交分别于点
的延长线交分别于点![]() 和
和![]() ,延长
,延长![]() 、
、![]() 相交于点
相交于点![]() ,那么
,那么![]() 的长度是________.
的长度是________.
【答案】![]()
【解析】
先证明AG=AF,由SSS得到△OHD与△OED全等,得出∠ODH=∠ODE=54°,证出∠B=∠C=72°,设GB=xcm,由△DHB∽△GBD,利用相似三角形对应边成比例列出比例式,求出x的值,即可得出结果.
:∵五边形DEFGH是正五边形,
∴∠HDE=∠DEF=∠EFG=∠FGH=∠GHD=108°,
∴∠BHD=∠CED=∠AGF=∠AFG=72°,
∴AG=AF,
∴△AGF是等腰三角形;
连接DG,如图所示:
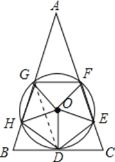
∵BC是⊙O的切线,
∴OD⊥BC,
∴∠BFO=∠CFO=90°,
在△OHD与△OED中,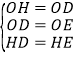 ,
,
∴△OHD≌△OED(SSS),
∴∠ODH=∠ODE=54°,
∴∠HDB=∠EDC=36°,
∴∠B=∠C=72°,
∴BD=DH=DE=DC=GF,
∴GF=![]() BC,
BC,
∵∠B=∠AGF=72°,
∴FG∥BC,
∴四边形FGDC是平行四边形,
∴GD∥CA,
∵BD=CD,
∴AG=GB,
∴点G是线段AB的中点;
∵五边形DEFGH是正五边形,
∴BD=DH=GH=2,
设GB=x,
∵∠BDH=∠BGD,∠B=∠B,
∴△DHB∽△GBD,
∴![]() ,即
,即![]() ,
,
整理得:x2-2x-4=0,
解得:x=1±![]() (负值舍去),
(负值舍去),
∴AG=GB=1+![]() ,
,
∴AB=2+2![]() ;
;
故答案为:2+2![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知点C与某建筑物底端B相距306米(点C与点B在同一水平面上),某同学从点C出发,沿同一剖面的斜坡CD行走195米至坡顶D处,斜坡CD的坡度(或坡比)i=1:2.4,在D处测得该建筑物顶端A的俯视角为20°,则建筑物AB的高度约为(精确到0.1米,参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364)( )
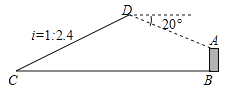
A. 29.1米 B. 31.9米 C. 45.9米 D. 95.9米
查看答案和解析>>
科目:初中数学 来源: 题型:
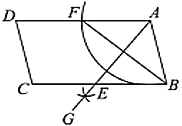
【题目】如图,在![]() 中,按以下步骤作图:①以
中,按以下步骤作图:①以![]() 为圆心,以
为圆心,以![]() 长为半径作弧,交
长为半径作弧,交![]() 于点
于点![]() ;②分别以
;②分别以![]() 、
、![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径作弧,两弧相交于点
的长为半径作弧,两弧相交于点![]() ;③作射线
;③作射线![]() ,交边
,交边![]() 于点
于点![]() .若
.若![]() ,
,![]() ,则
,则![]() 的长为_________.
的长为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是
是![]() 的内心,过点
的内心,过点![]() 作
作![]() ,与
,与![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() ,则( )
,则( )
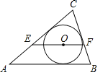
A. EF>AE+CF B. EF<AE+CF C. EF=AE+BF D. EF≤AE+CF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017重庆A卷第11题)如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).
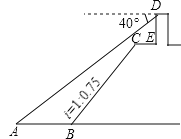
A. 5.1米 B. 6.3米 C. 7.1米 D. 9.2米
查看答案和解析>>
科目:初中数学 来源: 题型:
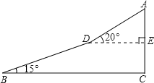
【题目】如图,一勘测人员从![]() 点出发,沿坡角为
点出发,沿坡角为![]() 的坡面以
的坡面以![]() 千米/时的速度行至
千米/时的速度行至![]() 点,用了
点,用了![]() 分钟,然后沿坡角为
分钟,然后沿坡角为![]() 的坡面以
的坡面以![]() 千米/时的速度到达山顶
千米/时的速度到达山顶![]() 点,用了
点,用了![]() 分钟.求山高(即
分钟.求山高(即![]() 的长度)及
的长度)及![]() 、
、![]() 两点的水平距离(即
两点的水平距离(即![]() 的长度)(精确到
的长度)(精确到![]() 千米).
千米).![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.

(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com