
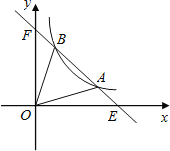
【题目】如图,直线![]() 与双曲线
与双曲线![]() 交于A、B两点,与x轴、y轴分别交于E、F两点,连接OA、OB,若
交于A、B两点,与x轴、y轴分别交于E、F两点,连接OA、OB,若![]()
![]() ,则
,则![]() ______.
______.
【答案】![]()
![]()
【解析】
试题根据直线解析式求出点E、F的坐标,过点O作OM⊥AB于点M,设A(x1,y1)、B(x2,y2),联立两函数解析式求解可得y1=x2,y2=x1,从而判断出点A、B关于OM对称,并求出点A的坐标,然后代入双曲线解析式计算即可得解.
解:令y=0,则﹣x+b=0,
解得x=b,
令x=0,则y=b,
所以,点E(b,0)、F(0,b),
所以,OE=OF,
过点O作OM⊥AB于点M,则ME=MF,

设点A(x1,y1)、B(x2,y2),
联立 ,
,
消掉y得,x2﹣bx+1=0,
根据根与系数的关系,x1x2=1,
所以y1y2=1,
所以y1=x2,y2=x1,
所以OA=OB,
所以AM=BM(等腰三角形三线合一),
∵S△AOB=S△OBF+S△OAE,
∴FB=BM=AM=AE,
所以点A(![]() b,
b,![]() b),
b),
∵点A在双曲线y=![]() 上,
上,
∴![]() b×
b×![]() b=1,
b=1,
解得b=![]()
![]() .
.
故答案为:![]()
![]() .
.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】某校为了解九年级学生体育测试情况,以九年级(1)班学生的体育测试成绩为样本,按A,B,C,D四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:

(说明:A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下)
(1)请把条形统计图补充完整;
(2)扇形统计图中D级所在的扇形的圆心角度数是多少?
(3)若该校九年级有600名学生,请用样本估计体育测试中A级学生人数约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【本小题满分9分】某校组织了一次初三科技小制作比赛,有A、B、C、D四个班共提供了100件参赛作品.C班提供的参赛作品的获奖率为50%,其他几个班的参赛作品情况及获奖情况绘制在下列图①和图②两幅尚不完整的统计图中.
(1)B班参赛作品有多少件?
(2)请你将图②的统计图补充完整;
(3)通过计算说明,哪个班的获奖率高?
(4)将写有A、B、C、D四个字母的完全相同的卡片放人箱中,从中一次随机抽出两张卡片,求抽到A、B两班的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
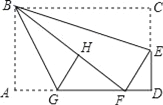
【题目】如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
①∠EBG=45°;②△DEF∽△ABG;③S△ABG=![]() S△FGH;④AG+DF=FG.
S△FGH;④AG+DF=FG.
其中正确的是__.(把所有正确结论的序号都选上)
查看答案和解析>>
科目:初中数学 来源: 题型:
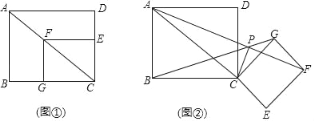
【题目】如图①,四边形ABCD与四边形CEFG都是矩形,点E,G分别在边CD,CB上,点F在AC上,AB=3,BC=4
(1)求![]() 的值;
的值;
(2)把矩形CEFG绕点C顺时针旋转到图②的位置,P为AF,BG的交点,连接CP
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)判断CP与AF的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知RtΔABC,∠C=90°,D为BC的中点.以AC为直径的圆O交AB于点E.
(1)求证:DE是圆O的切线.
(2)若AE:EB=1:2,BC=6,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
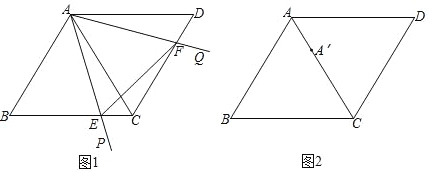
【题目】如图1,AC是边长为6的菱形ABCD的对角线,∠ABC=∠PAQ=60°,∠PAQ绕点A旋转,射线AP、AQ分别交边BC、CD于点E、F,连接EF.请探究:
(1)在旋转过程中,线段AE、AF有怎样的数量关系?并说明理由;
(2)在旋转过程中,△AEF的面积是否存在最小值?若存在,请求出最小值,若不存在,请说明理由
(3)如图2,将∠PAQ沿着AC向下平移至点A处,使CA′:AA′=2:1,在∠PA′Q绕点A′旋转过程中,始终保持∠ABC=∠PA′Q,射线A′P、A′Q分别交直线BC、CD于点E、F,连接EF.当S△A′EF:S菱形ABCD=19:18时,直接写出线段CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)如图,在一滑梯侧面示意图中,BD∥AF,BC⊥AF于点C,DE⊥AF于
点E.BC=1.8m,BD=0.5m,∠A=45,∠F=29.
(1)求滑道DF的长(精确到0.1m);
(2)求踏梯AB底端A与滑道DF底端F的距离AF(精确到0.1m).
(参考数据:sin29≈0.48,cos29≈0.87,tan29≈0.55)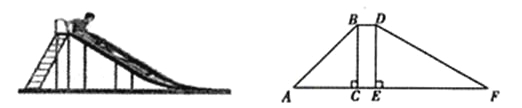
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com