
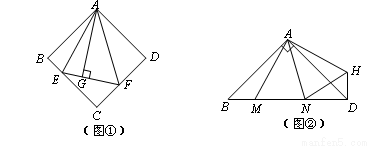
(1)如图①,在正方形ABCD中,△AEF的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,求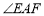 的度数.
的度数.
(2)如图②,在Rt△ABD中,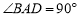 ,
,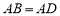 ,点M,N是BD边上的任意两点,且
,点M,N是BD边上的任意两点,且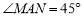 ,将△ABM绕点A逆时针旋转
,将△ABM绕点A逆时针旋转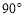 至△ADH位置,连接
至△ADH位置,连接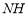 ,试判断MN,ND,DH之间的数量关系,并说明理由.
,试判断MN,ND,DH之间的数量关系,并说明理由.
(3)在图①中,连接BD分别交AE,AF于点M,N,若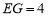 ,
,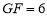 ,
,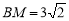 ,求AG,MN的长.
,求AG,MN的长.
(1) 45°.(2) MN2=ND2+DH2.理由见解析;(3)5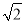 .
.
【解析】
试题分析:(1)根据高AG与正方形的边长相等,证明三角形全等,进而证明角相等,从而求出解.
(2)用三角形全等和正方形的对角线平分每一组对角的知识可证明结论.
(3)设出线段的长,结合方程思想,用数形结合得到结果.
试题解析:(1)在Rt△ABE和Rt△AGE中,AB=AG,AE=AE,
∴Rt△ABE≌Rt△AGE(HL).
∴∠BAE=∠GAE.
同理,∠GAF=∠DAF.
∴∠EAF=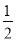 ∠BAD=45°.
∠BAD=45°.
(2)MN2=ND2+DH2.
∵∠BAM=∠DAH,∠BAM+∠DAN=45°,
∴∠HAN=∠DAH+∠DAN=45°.
∴∠HAN=∠MAN.
又∵AM=AH,AN=AN,
∴△AMN≌△AHN.
∴MN=HN.
∵∠BAD=90°,AB=AD,
∴∠ABD=∠ADB=45°.
∴∠HDN=∠HDA+∠ADB=90°.
∴NH2=ND2+DH2.
∴MN2=ND2+DH2.
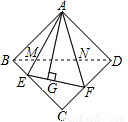
(3)由(1)知,BE=EG,DF=FG.
设AG=x,则CE=x-4,CF=x-6.
在Rt△CEF中,
∵CE2+CF2=EF2,
∴(x-4)2+(x-6)2=102.
解这个方程,得x1=12,x2=-2(舍去负根).
即AG=12.(8分)
在Rt△ABD中,
∴BD=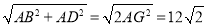 .
.
在(2)中,MN2=ND2+DH2,BM=DH,
∴MN2=ND2+BM2.
设MN=a,则a2=(12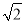 -3
-3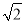 -a)2+(3
-a)2+(3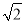 )2.
)2.
即a 2=(9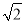 -a) 2+(3
-a) 2+(3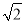 ) 2,
) 2,
∴a=5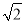 .即MN=5
.即MN=5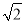 .
.
考点:1.正方形的性质;2.全等三角形的判定与性质;3.勾股定理.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源:2014-2015学年福建省南平市八年级上学期期中考试数学试卷(解析版) 题型:选择题
如图A、B、C三个居民小区的位置成三角形,现决定三个小区之间修建一个超市,使它到三个小区的距离相等,则超市应建在( )

A.AC,BC 的两条高线的交点处
B.∠A,∠B两内角平分线的交点处
C.AC、BC两边中线的交点处
D.AC、BC两条边垂直平分线的交点处
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省南平市八年级上学期期中考试数学试卷(解析版) 题型:解答题
(8分)如图,在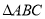 中,DE是AC的垂直平分线,AE=3cm,
中,DE是AC的垂直平分线,AE=3cm,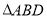 的周长为13cm,求
的周长为13cm,求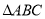 的周长
的周长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com