Question

【题目】如图，直线l1的解析式为y=-x+4，直线l2的解析式为y=x-2，l1和l2的交点为点B.

（1）直接写出点B坐标；

（2）平行于y轴的直线交x轴于点M，交直线l1于E，交直线l2于F.

①分别求出当x =2和x =4时E F的值.

②直接写出线段E F的长y与x的函数关系式，并画出函数图像L.

③在②的条件下，如果直线y=kx+b与L只有一个公共点，直接写出k的取值范围.

Answer 1

【答案】（1）（3，1）；（2）①EF=2；②见解析. ③k >2或k<-2或.k=-

【解析】（1）直接联立两个解析式求解即为点B的坐标.

（2）①当x=2时，分别求出点E、F的纵坐标即可解答.

当x=4时，分别求出点E、F的纵坐标即可解答.

②分两种情况讨论：当x或x时，线段E F的长y与x的函数关系式.

（1）联立两个解析式可得y=-x+4y=x-2，

解得x=3，y=1，∴点B的坐标为（3，1）；

（2）①如图：

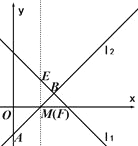
当x=2时，y=-x+4=2，∴E（2，2），

当x=2时，y=x-2=0，∴F（2，0），

∴EF=2；

如图：

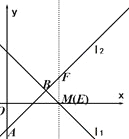
当x=4时，y=-x+4=0，∴E（4，0），

当x=4时，y=x-2=2，∴F（4，2），

∴EF=2；

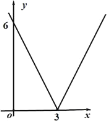
② L：，

图像如图所示：

③k >2或k<-2或.k=-.