
【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E. 
(1)求证:DC=DE;
(2)若tan∠CAB= ![]() ,AB=3,求BD的长.
,AB=3,求BD的长.
【答案】
(1)证明:连接OC,
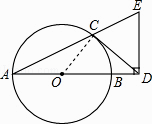
∵CD是⊙O的切线,
∴∠OCD=90°,
∴∠ACO+∠DCE=90°,
又∵ED⊥AD,∴∠EDA=90°,
∴∠EAD+∠E=90°,
∵OC=OA,∴∠ACO=∠EAD,
故∠DCE=∠E,
∴DC=DE
(2)解:设BD=x,则AD=AB+BD=3+x,OD=OB+BD=1.5+x,
在Rt△EAD中,
∵tan∠CAB= ![]() ,∴ED=
,∴ED= ![]() AD=
AD= ![]() (3+x),
(3+x),
由(1)知,DC= ![]() (3+x),在Rt△OCD中,
(3+x),在Rt△OCD中,
OC2+CD2=DO2,
则1.52+[ ![]() (3+x)]2=(1.5+x)2,
(3+x)]2=(1.5+x)2,
解得:x1=﹣3(舍去),x2=1,
故BD=1
【解析】(1)利用切线的性质结合等腰三角形的性质得出∠DCE=∠E,进而得出答案;(2)设BD=x,则AD=AB+BD=3+x,OD=OB+BD=1.5+x,利用勾股定理得出BD的长.


科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的为8,B是数轴上一点,且AB=14,动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
![]()
(1)写出数轴上点B表示的数 ,点P表示的数 (用含t的代数式表示);
(2)动点H从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、H同时出发,问点P运动多少秒时追上点H?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的运算程序中,若开始输入的x值为48,我们发现第1次输出的结果为24,第2次输出的结果为12,…第2019次输出的结果为( )

A. 3 B. 6 C. 12 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索与发现
(1)正方形ABCD中有菱形PEFG,当它们的对角线重合,且点P与点B重合时(如图1),通过观察或测量,猜想线段AE与CG的数量关系,并证明你的猜想;
(2)当(1)中的菱形PEFG沿着正方形ABCD的对角线平移到如图2的位置时,猜想线段AE与CG的数量关系,只写出猜想不需证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长CB1交直线l于点A1 , 作正方形A1B1C1B2 , 延长C1B2交直线l于点A2 , 作正方形A2B2C2B3 , 延长C2B3交直线l于点A3 , 作正方形A3B3C3B4 , …,依此规律,则A2016A2017= . 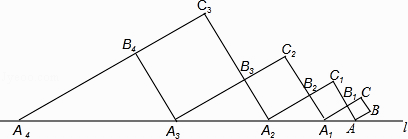
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把正整数1,2,3,…,2018排成如图所示的7列,规定从上到下依次为第1行、第2行、第3行、…,从左到右依次为第1至7列.
(1)数2018在第______行第______列;
(2)按如图所示的方法用方框框出四个数,这四个数的和能否为296?如果能,求出这四个数;如果不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1的解析式为y=-x+4,直线l2的解析式为y=x-2,l1和l2的交点为点B.

(1)直接写出点B坐标;
(2)平行于y轴的直线交x轴于点M,交直线l1于E,交直线l2于F.
①分别求出当x =2和x =4时E F的值.
②直接写出线段E F的长y与x的函数关系式,并画出函数图像L.
③在②的条件下,如果直线y=kx+b与L只有一个公共点,直接写出k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com