
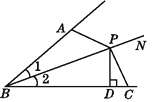
【题目】如图,∠1=∠2,P为BN上一点,且PD⊥BC于点D,AB+BC=2BD.试说明:∠BAP+∠BCP=180°.
【答案】见解析
【解析】作PE垂直于AB于E,根据角平分线的性质可知PD=PE,HL定理可知△PBD≌△PBE,可得BD=BE,根据题中线段和差的关系,可得△PAE≌△PCD,所以可知∠PAE=∠PCD,根据∠PAE+∠PAB=180°,即可证明题中关系.
证明:如图,过点P作PE⊥BA于E.
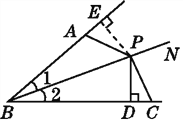
∵PD⊥BC,PE⊥BM,∠1=∠2,
∴PD=PE.
∵PD⊥BC,PE⊥BM,PD=PE,BP=BP,
∴△BPD≌△BPE.
∴BE=BD.
∵AB+BC=2BD,BC=BD+DC,AB=BE-AE,
∴AE=CD.
∵PD=PE,AE=CD,PD⊥BC,PE⊥BM,
∴△PCD≌△PAE,
∴∠PCB=∠PAE.
∵∠BAP+∠PAE=180°,
∴∠BAP+∠PCB=180°.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E. 
(1)求证:DC=DE;
(2)若tan∠CAB= ![]() ,AB=3,求BD的长.
,AB=3,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.
(1)图中除直角外,还有相等的角吗?请写出两对;
(2)如果∠AOD=50°,求∠DOP的度数.
(3)OP平分∠EOF吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠BAC=90°,D是AC的中点,CE⊥BD于点E,交BA的延长线于点F.若BF=12,则△FBC的面积为( )

A. 40 B. 46 C. 48 D. 50
查看答案和解析>>
科目:初中数学 来源: 题型:
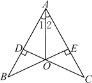
【题目】如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE与CD相交于点O,且∠1=∠2,则下列结论正确的个数为( )
①B=∠C;②△ADO≌△AEO;③△BOD≌△COE;④图中有四组三角形全等.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料后解决问题:
小明遇到下面一个问题:
计算(2+1)(22+1)(24+1)(28+1).
经过观察,小明发现如果将原式进行适当的变形后可以出现特殊的结构,进而可以应用平方差公式解决问题,具体解法如下:(2+1)(22+1)(24+1)(28+1)
=(2+1)(2﹣1)(22+1)(24+1)(28+1)
=(22﹣1)(22+1)(24+1)(28+1)
=(24﹣1)(24+1)(28+1)
=(28﹣1)(28+1)
=216﹣1
请你根据小明解决问题的方法,试着解决以下的问题:
(1)(2+1)(22+1)(24+1)(28+1)(216+1)=_____.
(2)(3+1)(32+1)(34+1)(38+1)(316+1)=_____.
(3)化简:(m+n)(m2+n2)(m4+n4)(m8+n8)(m16+n16).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=3a2b﹣2ab2+abc,小明同学错将“2A﹣B“看成”2A+B“,算得结果为4a2b﹣3ab2+4abc.
(1)计算B的表达式;
(2)求出2A﹣B的结果;
(3)小强同学说(2)中的结果的大小与c的取值无关,对吗?若a=![]() ,b=
,b=![]() ,
,
求(2)中式子的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租车从停车场出发,沿着东西向的大街行驶,到晚上6时,一天的行驶记录如下:(向东行驶记为正,向西行驶记为负,单位:千米)-4、+7、-9、+8、+6、-4、-3、+12
(1)到晚上6时,出租车在什么位置?
(2)若汽车每千米耗油0.2升,则从停车场出发到晚上6时,出租车共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AC=16,则图中长度为8的线段有( )

A. 2条 B. 4条 C. 5条 D. 6条
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com