
【题目】如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE与CD相交于点O,且∠1=∠2,则下列结论正确的个数为( )
①B=∠C;②△ADO≌△AEO;③△BOD≌△COE;④图中有四组三角形全等.
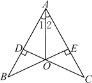
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】
先根据角平分线性质可得到OD=OE,根据垂直的定义得到∠BDO=∠CEO=90°,则可利用“ASA”判断△BDO≌△CEO,可得∠B=∠C;根据AAS可证△ABO≌△ACO;根据HL也可证△ADO≌△AEO,可得AD=AE;然后根据AAS,可证△ADC≌△AEB.
∵CD⊥AB,BE⊥AC,∠1=∠2,
∴OD=OE,∠BDO=∠CEO=90°,
在△BDO和△CEO中

∴△BDO≌△CEO(ASA),
∴∠B=∠C.
同理,根据全等三角形的判定:
由
得△ABO≌△ACO(AAS);
由![]()
得Rt△ADO≌Rt△AEO(HL);
由
得△ADC≌△AEB(AAS).
所以,共有4对全等三角形.
故选:D


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长CB1交直线l于点A1 , 作正方形A1B1C1B2 , 延长C1B2交直线l于点A2 , 作正方形A2B2C2B3 , 延长C2B3交直线l于点A3 , 作正方形A3B3C3B4 , …,依此规律,则A2016A2017= . 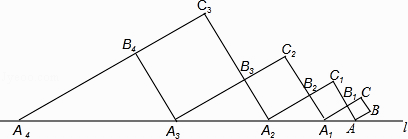
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点M,MN⊥AC于点N. 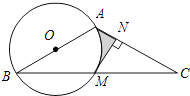
(1)求证:MN是⊙O的切线;
(2)若∠BAC=120°,AB=2,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店老板第一次用1000元购进一批文具,很快销售完毕;第二次购进时发现每件文具进价比第一次上涨了2.5元.老板用2500元购进了第二批文具,所购进文具的数量是第一次购进数量的2倍,同样很快销售完毕,两批文具的售价为每件15元.
(1)问第二次购进了多少件文具?
(2)文具店老板第一次购进的文具有30元的损耗,第二次购进的文具有125元的损耗,问文具店老板在这两笔生意中是盈利还是亏本?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直线L上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1、2、3,正放置的四个正方形的面积依次是![]() 、
、![]() 、
、![]() 、
、![]() ,则
,则![]() =( )
=( )
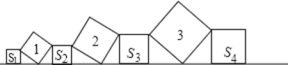
A. 5 B. 4 C. 6 D. 、10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角三角形,两条直角边分别为6cm,8cm,斜边长为10cm,若分别以一边旋转一周(①结果用π表示;②你可能用到其中的一个公式,V圆柱=πr2h,V球体=![]() ,V圆锥=
,V圆锥=![]() h)
h)
(1)如果绕着它的斜边所在的直线旋转一周形成的几何体是?
(2)如果绕着它的直角边6所在的直线旋转一周形成的几何体的体积是多少?
(3)如果绕着它的斜边10所在的直线旋转一周形成的几何体的体积与绕着直角边8所在的直线旋转一周形成的几何体的体积哪个大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )

A. 2对 B. 3对 C. 4对 D. 5对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.

(1)数轴上点A表示的数为________.
(2)将长方形OABC沿数轴水平移动,移动后的长方形记为O′A′B′C′,移动后的长方形O′A′B′C′与原长方形OABC重叠部分(如图2中阴影部分)的面积记为S.
①当S恰好等于原长方形OABC面积的一半时,数轴上点A′表示的数是多少?
②设点A的移动距离AA′=x.
(ⅰ)当S=4时,求x的值;
(ⅱ)D为线段AA′的中点,点E在线段OO′上,且OE=![]() OO′,当点D,E所表示的数互为相反数时,求x的值.
OO′,当点D,E所表示的数互为相反数时,求x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com