
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点M,MN⊥AC于点N. 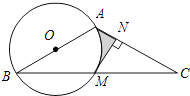
(1)求证:MN是⊙O的切线;
(2)若∠BAC=120°,AB=2,求图中阴影部分的面积.
【答案】
(1)解:证明:连接OM.
∵OM=OB,
∴∠B=∠OMB.
∵AB=AC,
∴∠B=∠C.
∴∠OMB=∠C.
∴OM∥AC.
∵MN⊥AC,
∴OM⊥MN.
∵点M在⊙O上,
∴MN是⊙O的切线

(2)解:连接AM.
∵AB为直径,点M在⊙O上,
∴∠AMB=90°.
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°.
∴∠AOM=60°.
又∵在Rt△AMC中,MN⊥AC于点N,
∴∠AMN=30°.
∴AN=AMsin∠AMN=ACsin30°sin30°= ![]() .
.
∴MN=AMcos∠AMN=ACsin30°cos30°= ![]() .
.
∴S梯形ANMO= ![]() ,
,
S扇形OAM= ![]() ,
,
∴S阴影= ![]() =
= ![]() ﹣
﹣ ![]() .
.
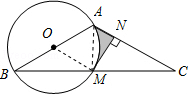
【解析】(1)有切点,需连半径,证明垂直,即可;(2)求阴影部分的面积要把它转化成S梯形ANMO﹣S扇形OAM , 再分别求的这两部分的面积求解.
【考点精析】掌握切线的判定定理和扇形面积计算公式是解答本题的根本,需要知道切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).


科目:初中数学 来源: 题型:
【题目】某公司从2014年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:
年度 | 投入技改资金 | 产品成本 |
2014 |
|
|
2015 | 3 | 12 |
2016 | 4 | 9 |
2017 |
| 8 |
(1)分析表中数据,请从一次函数和反比例函数中确定一个函数表示其变化规律,直接写出y与x的函数关系式;
(2)按照这种变化规律,若2018年已投入资金6万元.
①预计2018年每件产品成本比2017年降低多少万元?
②若计划在2018年把每件产品成本降低到5万元,则还需要投入技改资金多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,客轮在海上以30km/h的速度由B向C航行,在B处测得灯塔A的方向角为北偏东80°,测得C处的方向角为南偏东25°,航行1小时后到达C处,在C处测得A的方向角为北偏东20°,则C到A的距离是( )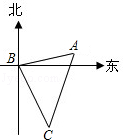
A.15 ![]() km
km
B.15 ![]() km
km
C.15( ![]() +
+ ![]() )km
)km
D.5( ![]() +3
+3 ![]() )km
)km
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,已知线段AB上有两点C,D,且AC=BD,M,N分别是线段AC,AD的中点,若AB=acm,AC=BD=bcm,且a,b满足(a-10)2+![]() =0.
=0.
![]()
(1)求AB,AC的长度;
(2)求线段MN的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,CE⊥AB 于 E,DF⊥AB 于 F,AC∥ED,CE 是∠ACB 的平分线, 则图中与∠FDB 相等的角(不包含∠FDB)的个数为( )

A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.
(1)图中除直角外,还有相等的角吗?请写出两对;
(2)如果∠AOD=50°,求∠DOP的度数.
(3)OP平分∠EOF吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
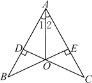
【题目】如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE与CD相交于点O,且∠1=∠2,则下列结论正确的个数为( )
①B=∠C;②△ADO≌△AEO;③△BOD≌△COE;④图中有四组三角形全等.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个梯子AB斜靠在一竖直的墙AO上,测得AO=2 m.若梯子的顶端沿墙下滑0.5米,这时梯子的底端也恰好外移0.5米,则梯子的长度AB为( )
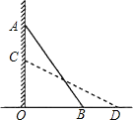
A. 2.5 m B. 3 m C. 1.5 m D. 3.5 m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com