解:(1)依题意,有:
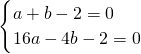
,解得

∴抛物线的解析式:y=

x
2-

x-2.
(2)由(1)的抛物线知:A(-1,0)、B(4,0)、C(0,-2),
∴OA=1,OC=2,AC=

=

;
直线AC:y=-2x-2.
通过图示可看出,当点M位于y轴右侧时,CM>AN,所以点M必在y轴右侧;
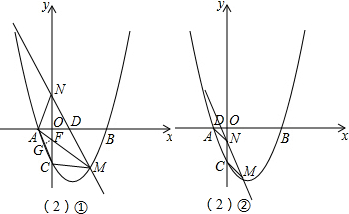
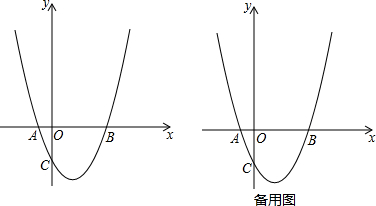
①当点N在x轴上方时,如图①;
此时,四边形ACMN是等腰梯形,则有:
∠MAC=∠NCA,tan∠MAC=tan∠NCA=

;
过点F作FG⊥AC于G,设FG=x,有:AG=GC=2x,AF=CF=

x;
∵AC=AG+GC=4x=

,x=

,FC=

x=

,
∴OF=OC-FC=2-

=

,F(0,-

);
∴直线AF:y=-

x-

,联立抛物线的解析式有:

,解得
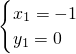
(舍)、
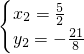
∴M(

,-
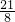
)
由于直线MN∥AC,设直线MN:y=-2x+h,则有:
-5+h=-
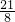
,h=
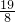
∴直线MN:y=-2x+
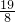
,则D(
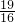
,0);
②当点N在x轴下方时,如图②,此时四边形ACMN是平行四边形;
∵点A、M关于CN的中点对称,∴点M的横坐标为 1,则M(1,-3);
同①可求得直线MN:y=-2x-1,得 D(-

,0);
综上,点D的坐标为(
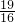
,0)或(-

,0).
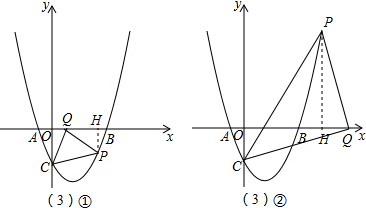
(3)由题意知:点P、Q都在y轴的右侧,可设Q(x,0)(x>0),过点P作PH⊥x轴于点H;
分两种情况讨论:
①点Q在点C、P之间,如图①;
∵△CPQ是等腰直角三角形,且CP是底边,
∴∠CQP=90°,CQ=QP;
∵

∴△CQO≌△QPH,则:PH=OQ=x,QH=OC=2,OH=OQ+QH=x+2
∴点P可表示为(x+2,-x),代入抛物线解析式有:
-x=

(x+2)
2-

(x+2)-2,解得 x=
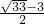
(负值舍去)
∴Q
1(
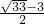
,0);
②点Q在点P右侧时,如图②;
同①可证得:△OCQ≌△HQP,∴HQ=CO=2,PH=OQ=x,OH=OQ-HQ=x-2,则 P(x-2,x);
代入抛物线解析式,有:
x=

(x-2)
2-

(x-2)-2,解得 x
1=
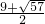
、x
2=
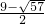
(舍,因为此时点P在y轴右侧)
∴Q
2(
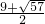
,0);
综上,存在符合条件的点Q,且坐标为(
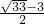
,0)、(
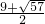
,0).
分析:(1)利用待定系数法求抛物线的解析式即可.
(2)直线DE与抛物线的交点有两个,通过观察图可看出,点M在y轴右侧时,一定不符合CM=AN的条件,所以只考虑点M在y轴右侧的情况:
①当点N在y轴上方时,MN∥AC,且AN=CM,显然四边形ACMN是等腰梯形,那么∠CAM=∠ACN,可过AM与y轴的交点作线段AC的垂线,在构建的两个小直角三角形中求出这个交点的坐标,进而能求出直线AM的解析式,联立抛物线解析式即可得到点M的坐标,而直线MN与直线AC平行,那么它们的斜率相同,可根据这个条件先设出直线MN的解析式,代入点M的坐标后,进一步能求出点D的坐标;
②当点N在y轴下方时,显然四边形ACMN是平行四边形,那么点A、M的横坐标互为相反数(由于CN在y轴上,而A、M关于CN的中点对称),可先将点M的横坐标代入抛物线解析式中确定点M的坐标,然后按①的思路求出点D的坐标.
(3)由于抛物线向x轴正方形平移,那么点P必在y轴右侧,若△CPQ是以CP为斜边的等腰直角三角形,那么点Q必须在x轴正半轴上,然后分两种情况讨论:
①点Q在点C、P之间时;②点Q在点P的右侧时;
解题思路相同,先设出点Q的坐标,过点P作x轴的垂线,通过构建的全等三角形(这里要用到等腰直角三角形的顶角为90°以及腰相等这两个条件),先表示出点P的坐标(用点Q的横坐标来表示),代入抛物线解析式后,即可确定点Q的坐标.
点评:此题主要考查了利用待定系数法确定函数解析式、特殊四边形的判定和性质、相似三角形与全等三角形的应用等重点知识;这道题的思路和解答过程相等复杂,需要辅以图形来解答题目,在作图时,可以将与所做小题无关的图形去掉,这样可以更直观的看出线段、图形间的位置、数量关系.另外,后两题涉及的情况较多,一定要注意分类讨论.

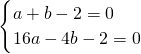 ,解得
,解得
 x2-
x2- x-2.
x-2. =
= ;
; ①当点N在x轴上方时,如图①;
①当点N在x轴上方时,如图①; ;
; x;
x; ,x=
,x= ,FC=
,FC= x=
x= ,
, =
= ,F(0,-
,F(0,- );
); x-
x- ,联立抛物线的解析式有:
,联立抛物线的解析式有: ,解得
,解得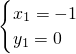 (舍)、
(舍)、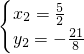
 ,-
,-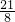 )
)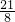 ,h=
,h=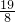
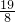 ,则D(
,则D(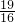 ,0);
,0); ,0);
,0);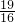 ,0)或(-
,0)或(- ,0).
,0). (3)由题意知:点P、Q都在y轴的右侧,可设Q(x,0)(x>0),过点P作PH⊥x轴于点H;
(3)由题意知:点P、Q都在y轴的右侧,可设Q(x,0)(x>0),过点P作PH⊥x轴于点H;
 (x+2)2-
(x+2)2- (x+2)-2,解得 x=
(x+2)-2,解得 x=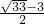 (负值舍去)
(负值舍去)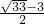 ,0);
,0); (x-2)2-
(x-2)2- (x-2)-2,解得 x1=
(x-2)-2,解得 x1=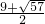 、x2=
、x2=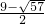 (舍,因为此时点P在y轴右侧)
(舍,因为此时点P在y轴右侧)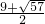 ,0);
,0);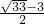 ,0)、(
,0)、(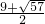 ,0).
,0).

 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少? O为坐标原点,抛物线上一点C的横坐标为1.
O为坐标原点,抛物线上一点C的横坐标为1. 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, 与x轴交于点A、B,点A的坐标为(-2,0).
与x轴交于点A、B,点A的坐标为(-2,0).