
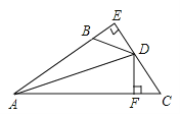
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,∠ABD与∠C互补.
(1)求证:AD平分∠BAC;(2)若AB=5,AC=9,则AE=_________.
【答案】见解析
【解析】(1)首先证明Rt△BED≌Rt△CED,根据全等三角形的对应边相等证明DE=DF,即可证得AD是∠BAC的平分线;
(2)根据全等三角形的性质得到AF=AE,BE=CF,根据AE=AC-CF=AB+BE,得到BE=2,于是得到结论.
解:(1)证明:∵DE⊥AB于E,DF⊥AC于F,
∴∠E=∠DFC=90°,
∵∠ABD与∠C互补
∴∠ABD+∠C=180°
∵∠ABD+∠DBE=180°
∴∠DBE=∠C
∵BD=CD
∴△BDE≌△CDF(AAS)
∴DE=DF,即AD平分∠BAC;
(2)解:在△ADE与△ADF中,∠DAE=∠DAF,∠AED=∠AFD=90°,AD=AD,
∴AF=AE,
∵Rt△BED≌Rt△CFD,
∴BE=CF,∴AE=AC-CF=AB+BE,
∴BE=2,
∴AE=AB+BE=7.
故答案为:7.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某同学使用计算器求15个数据的平均数时,错将一个数据15输成105,那么由此求出的平均数与实际平均数的差是( )
A.6.5
B.6
C.0.5
D.-6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,E、F分别是AD和AD延长线上的点,DE=DF,连接BF、CE,下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.
其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某招聘考试分笔试和面试两种,其中笔试按60%、面试按40%计算加权平均数,作为总成绩.孔明笔试成绩90分,面试成绩85分,那么孔明的总成绩是分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察如图所示的图形,写出下列问题的结果:

(1)这个图形的名称是 ;
(2)这个几何体有 个面,有 个底面,有 个侧面,底面是 形,侧面是 形.
(3)侧面的个数与底面多边形的边数有什么关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,AC=8 cm,CB=6 cm,点M、N分别是AC、BC的中点.
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a cm,其它条件不变,你能猜想MN的长度吗?并说明理由;
(3)若C在线段AB的延长线上,且满足AC﹣BC=bcm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由;
(4)你能用一句简洁的话,描述你发现的结论吗?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算正确的是( )
A. 2aa = 2 B. 2a + b = 2ab C. 3x2 + 2x2 = 5x4 D. mn 2mn = mn
查看答案和解析>>
科目:初中数学 来源: 题型:
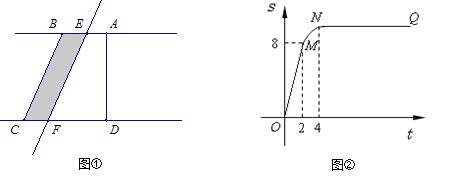
【题目】如图①所示,在直角梯形ABCD中,∠BAD=90°,E是直线AB上一点,过E作直线![]() //BC,交直线CD于点F.将直线
//BC,交直线CD于点F.将直线![]() 向右平移,设平移距离BE为
向右平移,设平移距离BE为![]() (t
(t![]() 0),直角梯形ABCD被直线
0),直角梯形ABCD被直线![]() 扫过的面积(图中阴影部份)为S,S关于
扫过的面积(图中阴影部份)为S,S关于![]() 的函数图象如图②所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
的函数图象如图②所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
信息读取
(1)梯形上底的长AB= ;(2) 直角梯形ABCD的面积= ;
图象理解
(3)写出图②中射线NQ表示的实际意义;(4) 当![]() 时,求S关于
时,求S关于![]() 的函数关系式;
的函数关系式;
问题解决
(5)当t为何值时,直线l将直角梯形ABCD分成的两部分面积之比为1: 3.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com