
����С������12�֣���ͼ1��ʾ����֪�ڡ�ABC�͡�DEF�У�AB��EF����B����E��EC��BD��

��1����˵������ABC�ա�FED��
��2����ͼ�ξ���ƽ�ƺ���ת��õ�ͼ2�����С�EDB��25º����A��66º�������AMD�Ķ�����

��3����ͼ�μ�����ת��õ�ͼ3����ʱD��B��F������ͬһ��ֱ���ϣ���DB��2DF������EB����֪��EFB�����Ϊ5cm2����������ı���ABED����������ܣ���������������ܣ�����˵�����ɡ�

������
��������
�����������1����EC=BD����ʽ�������߶�����DC���õ�ED=BC�����ɡ�B=��E��AB=EF������SAS��֤��������ABC��������FEDȫ�ȣ�
��2����������ABC��������FEDȫ�ȣ�����ȫ�������εĶ�Ӧ����ȣ��õ���EDF=��BDA���Ⱥ����߶���ȥ��BDF���õ���EDB=��ADF���ɡ�EDB�Ķ����õ���ADF�Ķ�������������AMD�У��ɡ�ADF����A�Ķ��������������ε��ڽǺͶ������������AMD�Ķ�����
��3����BD=2DF���õ�ΪDB���е㣬�ɵ�DF=BF�����õȵ�ͬ�߿ɵ�������DEF��������EFB�����ȣ���������ABD��������DEFȫ�ȣ��õ�������ABD��������DEF�����ȣ��ɵ�������DEF��������EFB��������ABD���������ȣ���������EFB������ɵó������������ε������������ӿɵó��ı���ABED�������
�����������1����EC=BD����֪����
��EC+CD=BD+DC����ED=BC��
�ڡ�ABC�͡�FED�У�
 ��
��
���ABC�ա�FED��SAS����
��2���ߡ�ABC�ա�FED��
���EDF=��BDA��
���EDF����BDF=��BDA����BDF���֡�EDB=25�㣬
���EDB=��ADF=25�㣬�֡�A=66�㣬
���AMD=180�㩁66�㩁25��=89�㣻
��3��������ı���ABED�����������Ϊ��
�ߡ�ABC�ա�FED��
��S��ABC=S��FED��
��DB=2DF����FΪBD�е㣬
��DF=BF����S��EFB=5��
��S��EDF=S��EFB=S��ABC=5��
��SABCD=S��EDF+S��EFB+S��ABC=15��
���㣺ȫ�������ε��ж�������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ���꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
ʵ��a��b��c�������ϵĶ�Ӧ���λ����ͼ��ʾ������ 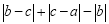 =___________��
=___________��
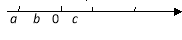
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ���꼶��ѧ�ڵڶ����¿���ѧ�Ծ��������棩 ���ͣ�ѡ����
��314�� ��
�� ��
�� ��02020020002��������������������� ��
��02020020002��������������������� ��
A��1�� B��2�� C 3�� D4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ��ɽ��ʡ�����о��꼶��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ�ѡ����
��ͼ��AB��CD��BO��OC=1��4����E��F�ֱ���OC��OD���е㣬��EF��AB��ֵΪ�� ��
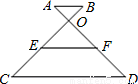
A��1 B��2 C��3 D��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ��ɽ��ʡ�����о��꼶��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ�ѡ����
��x1��x2��һԪ���η���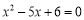 ������������
������������ ��ֵ�ǣ� ��
��ֵ�ǣ� ��
A��1 B��5 C�� D��6
D��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ���㽭ʡ�����а��꼶10���¿���ѧ�Ծ��������棩 ���ͣ������
����С������6�֣���ͼ����֪��ABF�ա�DEC����AC��DF��˵����ABC�ա�DEF�����ɣ�
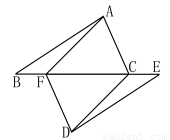
��������
�ߡ�ABF�ա�DEC
��AB�� ��BF��
�֡�BC��BF�� ��EF��CE�� ��
��BC�� ��
�ڡ�ABC���DEF��
���ABC�ա�DEF�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ���㽭ʡ�����а��꼶10���¿���ѧ�Ծ��������棩 ���ͣ�ѡ����
һ�������β�����С��������Ŀ飬��ͼ��С��ֻ�����е�����ȥ�����꣬����һ�����ǰһ���IJ���������Ϊ����������ȥ�������ˣ� ��

A���������������
B�����٣��ܻ�ۣ��ܾͿ�����
C�����٣��ܻ�ڣ��ܾͿ�����
D�����٣��ܻ�ڣ��ܻ�ۣ��ܾ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ���Ĵ�ʡ�㰲���ذ������������꼶12��������ѧ�Ծ��������棩 ���ͣ������
������8�֣���֪y= ����
���� ������ƽ������
������ƽ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ���������꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ�ѡ����
��ͼ��ͼ������ĵ�λ����Ϊ1�������B��C��ʾ�����ľ���ֵ��ȣ���ô��A���D��ʾ�����ֱ��ǣ� ��

A����2��2 B����4 , 1 C����5 , 1 D����6 , 2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com