

���� ��ͼ1���Ѧ����·��������������У�ʹ�á�ABD=������CBE=�£���BA��BC��ֱ��BD�����࣬����AC����֤�á�ABC�ǵ��������Σ�����æ�+��=��ABC=45��
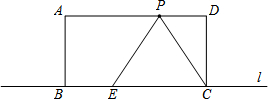
��ͼ2���Ѧ����·��������������У�ʹ�á�MOG=������NOH=�£���ON�ڡ�MOG�ڣ�����MN����֤�á�MON�ǵ��������Σ�����æ�-��=45�㣮
��� 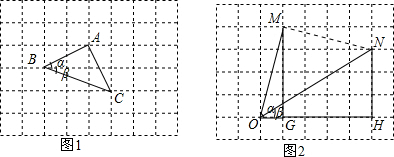 �⣺��ͼ1���Ѧ����·��������������У�ʹ�á�ABD=������CBE=�£���BA��BC��ֱ��BD�����࣬����AC����֤�á�ABC�ǵ��������Σ���˿���æ�+��=��ABC=45�㣻
�⣺��ͼ1���Ѧ����·��������������У�ʹ�á�ABD=������CBE=�£���BA��BC��ֱ��BD�����࣬����AC����֤�á�ABC�ǵ��������Σ���˿���æ�+��=��ABC=45�㣻
�ο�С��˼������ķ���������⣺
��������¶�Ϊ��ǣ���tan��=4��tan��=$\frac{3}{5}$ʱ����ͼ2�������������У���������������Ǧ���������MON=��-�£��ɴ˿ɵæ�-��=45�㣮
�ʴ�Ϊ��45��45
���� ���⿼������ͼ-Ӧ�������ͼ�����������ε����ʣ���ֱ�������εȣ����ݺ���ֵ����ֱ���������ǽ���Ĺؼ���


 ͬ����ϰǿ����չϵ�д�
ͬ����ϰǿ����չϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017�����ʡ����о��꼶��ѧ�ڵ�һ��ģ�⣨���У�������ѧ�Ծ��������棩 ���ͣ�ѡ����
���㵺���й��Ĺ���������λ���й����������Լ4400000ƽ���ף�����4400000�ÿ�ѧ��������ʾΪ
A��44��105 B��0.44��105 C��4.4��106 D��4.4��105
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�콭��ʡ���꼶��ѧ�ڵ�һ��ģ�⿼����ѧ�Ծ��������棩 ���ͣ������
��2013•��������һ��Բ�Ľ�Ϊ120�㣬�뾶Ϊ4��������һ��Բ�IJ��棬���Բ�ĵ���Բ�İ뾶Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ����ABCD�ı�BC��ֱ��l�ϣ�AB=2��BC=4��P��AD����һ�����Ҳ����D�غϣ�����CP������P����APE=��CPD����ֱ��l�ڵ�E����PD�ij�Ϊx����PEC�����ABCD�غϲ��ֵ����Ϊy��������ͼ���У��ܱ�ʾy��x�ĺ�����ϵ��ͼ������ǣ�������
����ABCD�ı�BC��ֱ��l�ϣ�AB=2��BC=4��P��AD����һ�����Ҳ����D�غϣ�����CP������P����APE=��CPD����ֱ��l�ڵ�E����PD�ij�Ϊx����PEC�����ABCD�غϲ��ֵ����Ϊy��������ͼ���У��ܱ�ʾy��x�ĺ�����ϵ��ͼ������ǣ�������| A�� | 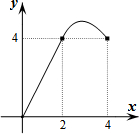 | B�� | 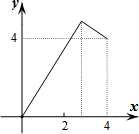 | C�� | 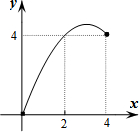 | D�� | 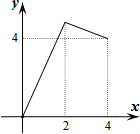 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
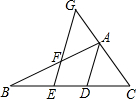 ��֪����ͼ��AD�ǡ�ABC��ƽ���ߣ���E��BC�ϣ���G��CA���ӳ����ϣ�EG��AB�ڵ�F����GE��AD����֤����AFG=��G��
��֪����ͼ��AD�ǡ�ABC��ƽ���ߣ���E��BC�ϣ���G��CA���ӳ����ϣ�EG��AB�ڵ�F����GE��AD����֤����AFG=��G���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
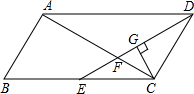 ��ͼ��?ABCD�У�AB=3cm��AD=6cm����ADC�Ľ�ƽ����DE��BC�ڵ�E����AC�ڵ�F��CG��DE������ΪG��DG=$\frac{3}{2}\sqrt{3}$cm����EF�ij�Ϊ��������
��ͼ��?ABCD�У�AB=3cm��AD=6cm����ADC�Ľ�ƽ����DE��BC�ڵ�E����AC�ڵ�F��CG��DE������ΪG��DG=$\frac{3}{2}\sqrt{3}$cm����EF�ij�Ϊ��������| A�� | 2cm | B�� | $\sqrt{3}$cm | C�� | 1cm | D�� | $\frac{2}{3}\sqrt{3}$cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com