练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．当x是满足-2≤x≤2的整数时，求代数式（$\frac{3}{x-2}$+$\frac{2}{x+2}$）÷$\frac{5{x}^{2}+2x}{{x}^{2}-4}$的值．

    分析 原式括号中两项通分并利用同分母分式的加法法则计算，同时利用除法法则变形，约分得到最简结果，把x的值代入计算即可求出值．

    解答 解：原式=$\frac{3（x+2）+2（x-2）}{（x+2）（x-2）}$•$\frac{（x+2）（x-2）}{x（5x+2）}$=$\frac{5x+2}{x（5x+2）}$=$\frac{1}{x}$，
    ∵x是满足-2≤x≤2的整数，
    ∴x可以取1，-1．
    当x=1时，原式=1；
    当x=-1时，原式=-1．

    点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    20．阅读下面的材料
    小敏在数学课外小组活动中遇到这样一个问题：
    如果α，β都为锐角，且tanα=$\frac{1}{2}$，tan$β=\frac{1}{3}$，求α+β的度数．
    小敏是这样解决问题的：如图1，把α，β放在正方形网格中，使得∠ABD=α，∠CBE=β，且BA，BC在直线BD的两侧，连接AC，可证得△ABC是等腰三角形，因此可求得α+β=∠ABC=45°
    请参考小敏思考问题的方法解决问题：
    如果α，β都为锐角，当tanα=4，tanβ=$\frac{3}{5}$时，在图2的正方形网格中，利用已作出的锐角α，画出∠MON=α-β，由此可得α-β=45°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

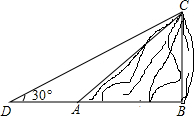    1．如图，某人在D处测得山顶C的仰角为30°，向前走30米到达山脚A处，测得山坡AC的坡度为i=1：1.5，求山顶的高度（不计测角仪的高度，$\sqrt{3}$≈1.73，结果保留整数）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．下列说法正确的是（　　）
    A．两点之间的距离是两点间的线段
    B．同一平面内，过一点有且只有一条直线与已知直线平行
    C．与同一条直线垂直的两条直线也垂直
    D．同一平面内，过一点有且只有一条直线与已知直线垂直

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．函数y=$\frac{\sqrt{2-x}}{x}$的自变量取值范围是x≤2且x≠0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．下列计算正确的是（　　）
    A．（-3a）2=-9a2B．$\frac{-a+b}{a+b}$=-1C．2a2-1=（2a+1）（2a-1）D．a3-4a3=-3a3

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．下列各数等于3的是（　　）
    A．-$\sqrt{{3}^{2}}$B．-$\sqrt{（-3）^{2}}$C．（-$\sqrt{\frac{1}{3}}$）2D．$\sqrt{（-\frac{1}{3}）^{-2}}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．已知双曲线y=$\frac{k}{x}$和直线y=ax+b相交于A（-1，4）和B（2，m）两点，试确定双曲线和直线的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．已知a＜b，二次根式$\sqrt{-{a}^{3}b}$化简为（　　）
    A．a$\sqrt{ab}$B．a$\sqrt{-ab}$C．-a$\sqrt{ab}$D．-a$\sqrt{-ab}$

    查看答案和解析>>

    同步练习册答案