
【题目】如图,△ABC的三边AB,BC,CA的长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO∶S△BCO∶S△CAO等于( )
A.1∶1∶1
B.1∶2∶3
C.2∶3∶4
D.3∶4∶5
【答案】C
【解析】解:过点O作OE⊥AB于点E,OF⊥BC于点F,OD⊥AC于点D,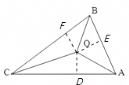
∵OA,OB,OC分别是△ABC三内角的角平分线,
∴OE=OF=OD ,
∵S△ABO=![]() AB·OE =10OE, S△BCO=
AB·OE =10OE, S△BCO=![]() BC·OF=15OF ,S△CAO=
BC·OF=15OF ,S△CAO=![]() AC·OD=20OD,
AC·OD=20OD,
∴S△ABO∶S△BCO∶S△CAO=10OE∶15OF∶20OD=2∶3∶4
故应选:C.
根据角平方线上的点到角两边的距离相等得出OE=OF=OD ,根据三角形的面积法,得出S△ABO=![]() AB·OE =10OE, S△BCO=
AB·OE =10OE, S△BCO=![]() BC·OF=15OF ,S△CAO=
BC·OF=15OF ,S△CAO=![]() AC·OD=20OD,从而得出答案S△ABO∶S△BCO∶S△CAO=10OE∶15OF∶20OD=2∶3∶4 。
AC·OD=20OD,从而得出答案S△ABO∶S△BCO∶S△CAO=10OE∶15OF∶20OD=2∶3∶4 。


科目:初中数学 来源: 题型:
【题目】国庆60周年阅兵式上,向世界展示了一种新型导弹―“红-九地空导弹”.它是我国自行研制的远程防空导弹,集美俄技术于一身,以拦截飞机为主,同时具有很强的拦截短程弹道导弹的能力.10枚“红-九地空导弹”(每枚底面的直径均为0.4m)以如图方式堆放,为了防雨,需要搭建防雨棚,这个防雨棚的最低高度应为多少米(精确到0.1m)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线.
(2)求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
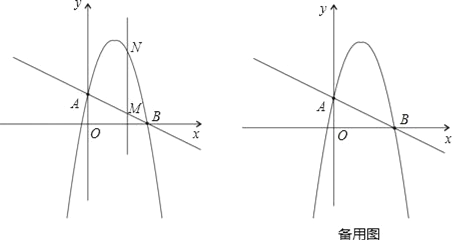
【题目】如图,一次函数![]() 分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一只不透明的盒子里有背面完全相同,正面上分别写有数字1、2、3、4的四张卡片,小马从中随机地抽取一张,把卡片上的数字作为被减数;在另一只不透明的盒子里将形状、大小完全相同,分别标有数字1、2、3的三个小球混合后,小虎从中随机地抽取一个,把小球上的数字做为减数,然后计算出这两个数的差.
(1)请你用画树状图或列表的方法,求这两数差为0的概率;
(2)小马与小虎做游戏,规则是:若这两数的差为非正数,则小马赢;否则小虎赢.你认为该游戏公平吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com