
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,结果为F(n)=3n+1;②当n为偶数时,结果为F(n)=![]() (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行.例如,取n=13,则:
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行.例如,取n=13,则:
![]()
若n=24,则第100次“F”运算的结果是_____
【答案】4
【解析】
根据题意,写出前几次的运算结果,发现其中的规律,通过计算得出从第5次开始,结果就只有1、4两个数循环出现,进而观察规律即可得结论.
解:当n=24,则第1次“F”运算的结果是:![]() =3,
=3,
第2次“F”运算的结果是:3n+1=10,
第3次“F”运算的结果是:![]() =5,
=5,
第4次“F”运算的结果是:3n+1=16,
第5次“F”运算的结果是:![]() =1,
=1,
第6次“F”运算的结果是:3n+1=4,
第7次“F”运算的结果是:![]() =1,
=1,
第8次“F”运算的结果是:3n+1=4,
…
观察以上结果,从第5次开始,结果就只有1、4两个数循环出现,
且当次数为奇数时,结果是1,次数为偶数时,结果是4,
而第100次是偶数,所以最后结果是4.
故答案为:4.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D竖起标杆DE,使得点E与点C、A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D、F、E、G都在△ABC的边上,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.(请在下面的空格处填写理由或数学式)
解:∵EF∥AD,(已知)
∴∠2= ( )
∵∠1=∠2,(已知)
∴∠1= ( )
∴ ∥ ,( )
∴∠AGD+ =180°,(两直线平行,同旁内角互补)
∵ ,(已知)
∴∠AGD= (等式性质)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某运输部门规定:办理托运,当一种物品的重量不超过16千克时,需付基础费30元和保险费a元:为限制过重物品的托运,当一件物品超过16千克时,除了付以上基础费和保险费外,超过部分每千克还需付b元超重费.设某件物品的重量为x千克.
(1)当x≤16时,支付费用为__________________元(用含a的代数式表示);
当x≥16时,支付费用为_________________元(用含x和a、b的代数式表示);
(2)甲、乙两人各托运一件物品,物品重量和支付费用如下表所示
物品重量(千克) | 支付费用(元) |
18 | 39 |
25 | 53 |
试根据以上提供的信息确定a,b的值.
(3)根据这个规定,若丙要托运一件超过16千克的物品,但支付的费用不想超过70元,那么丙托运的物品最多是多少千克.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() ,与x轴交于A、B两点(点A在点B的左侧).
,与x轴交于A、B两点(点A在点B的左侧).
(1)求点A和点B的坐标;
(2)若点P(m,n)是抛物线上的一点,过点P作x轴的垂线,垂足为点D.
①在![]() 的条件下,当
的条件下,当![]() 时,n的取值范围是
时,n的取值范围是![]() ,求抛物线的表达式;
,求抛物线的表达式;
②若D点坐标(4,0),当![]() 时,求a的取值范围.
时,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
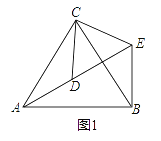
(1)证明:AD=BE;
(2)求∠AEB的度数.
问题变式:
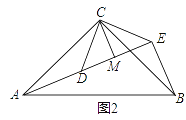
(3)如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.(Ⅰ)请求出∠AEB的度数;(Ⅱ)判断线段CM、AE、BE之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
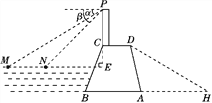
【题目】某水库大坝的横截面是如图所示的四边形ABCD,其中AB∥CD.大坝顶上有一瞭望台PC,PC正前方有两艘渔船M,N.观察员在瞭望台顶端P处观测到渔船M的俯角α为31°,渔船N的俯角β为45°.已知MN所在直线与PC所在直线垂直,垂足为E,且PE长为30米.
(1)求两渔船M,N之间的距离(结果精确到1米).
(2)已知坝高24米,坝长100米,背水坡AD的坡度i=1∶0.25.为提高大坝防洪能力,请施工队将大坝的背水坡通过填筑土石方进行加固,坝底BA加宽后变为BH,加固后背水坡DH的坡度i=1∶1.75.施工队施工10天后,为尽快完成加固任务,施工队增加了机械设备.工作效率提高到原来的2倍,结果比原计划提前20天完成加固任务,施工队原计划平均每天填筑土石方多少立方米?
(参考数据:tan 31°≈0.60,sin 31°≈0.52)
查看答案和解析>>
科目:初中数学 来源: 题型:
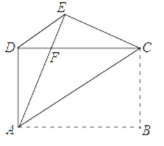
【题目】如图,在长方形ABCD中,AB>BC,把长方形沿对角线AC所在直线折叠,使点B落在点E处,AE交CD于点F,连接DE
求证:(1)△AED≌△CDE
(2)△EFD是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 于点
于点![]() ,
,![]() .
.
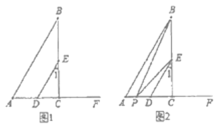
(1)求证:![]() ;
;
(2)如图2,点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 运动到点
运动到点![]() 停止,连接
停止,连接![]() 、
、![]() .则
.则![]() 、
、![]() 、
、![]() 三个角之间具有怎样的数量关系(不考虑点
三个角之间具有怎样的数量关系(不考虑点![]() 与点
与点![]() ,
,![]() ,
,![]() 重合的情况)?并说明理由.
重合的情况)?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com