
【题目】某运输部门规定:办理托运,当一种物品的重量不超过16千克时,需付基础费30元和保险费a元:为限制过重物品的托运,当一件物品超过16千克时,除了付以上基础费和保险费外,超过部分每千克还需付b元超重费.设某件物品的重量为x千克.
(1)当x≤16时,支付费用为__________________元(用含a的代数式表示);
当x≥16时,支付费用为_________________元(用含x和a、b的代数式表示);
(2)甲、乙两人各托运一件物品,物品重量和支付费用如下表所示
物品重量(千克) | 支付费用(元) |
18 | 39 |
25 | 53 |
试根据以上提供的信息确定a,b的值.
(3)根据这个规定,若丙要托运一件超过16千克的物品,但支付的费用不想超过70元,那么丙托运的物品最多是多少千克.
科目:初中数学 来源: 题型:
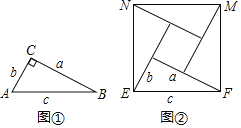
【题目】如图①,在Rt△ABC中,∠C=90°,两条直角边长分别为a,b,斜边长为c.如图②,现将与Rt△ABC全等的四个直角三角形拼成一个正方形EFMN.
(1)若Rt△ABC的两直角边之比均为2:3.现随机向该图形内掷一枚小针,则针尖落在四个直角三角形区域的概率是多少?
(2)若正方形EFMN的边长为8,Rt△ABC的周长为18,求Rt△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
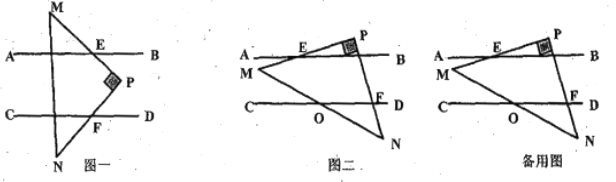
【题目】如图,已知![]() ,现将一直角三角形
,现将一直角三角形![]() 放入图中,其中
放入图中,其中![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
(1)当![]() 所放位置如图一所示时,则
所放位置如图一所示时,则![]() 与
与![]() 的数量关系为 ;
的数量关系为 ;
(2)当![]() 所放位置如图二所示时,试说明:
所放位置如图二所示时,试说明:![]() ;
;
(3)在(2)的条件下,若![]() 与
与![]() 交于点
交于点![]() ,且
,且![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
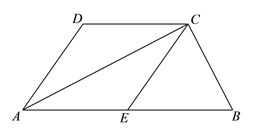
【题目】如图,已知△ACB中,∠ACB=90°,CE是△ACB的中线,分别过点A、点C作CE和AB的平行线,交于点D.
(1)求证:四边形ADCE是菱形;
(2)若CE=4,且∠DAE=60°,求△ACB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知点A(0,a),点B(b,0),其中a,b满足![]() =0,点C(m,n)在第一象限,已知
=0,点C(m,n)在第一象限,已知![]() 是2的立方根.
是2的立方根.

(1)直接写出A,B,C三点的坐标;
(2)求出△ABC的面积;
(3)如图2,延长BC交y轴于D点,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,结果为F(n)=3n+1;②当n为偶数时,结果为F(n)=![]() (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行.例如,取n=13,则:
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行.例如,取n=13,则:
![]()
若n=24,则第100次“F”运算的结果是_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为提高学生的身体素质,经常在课间开展学生跳绳比赛,下表为该校七年级![]() 班
班![]() 名学生参加某次跳绳比赛的情况,规定标准数量为每人每分钟
名学生参加某次跳绳比赛的情况,规定标准数量为每人每分钟![]() 个.
个.
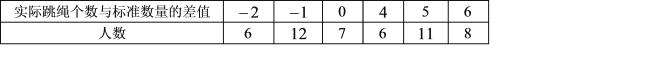
(1)求七年级![]() 班
班![]() 人中跳绳最多的同学一分钟跳的次数是多少个,跳绳最少的同学一分钟跳的次数是多少个?
人中跳绳最多的同学一分钟跳的次数是多少个,跳绳最少的同学一分钟跳的次数是多少个?
(2)跳绳比赛的计分方式如下:
①若每分钟跳绳个数是规定标准数量,不计分;
②若每分钟跳绳个数超过规定标准数量,每多跳![]() 个绳加
个绳加![]() 分
分
③若每分钟跳绳个数没有达到规定标准数量,每少跳![]() 个绳扣
个绳扣![]() 分
分
如果班级跳绳总积分超过![]() 分,便可得到学校的奖励,请你通过计算说明七年级
分,便可得到学校的奖励,请你通过计算说明七年级![]() 班能否得到学校奖励?
班能否得到学校奖励?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】字母m、n分别表示一个有理数,且m≠n.现规定min{m,n}表示m、n中较小的数,例如:min{3,﹣1}=﹣1,min{﹣1,0}=﹣1.据此解决下列问题:
(1)min{﹣![]() ,﹣
,﹣![]() }= .
}= .
(2)若min{![]() ,2)=﹣1,求x的值;
,2)=﹣1,求x的值;
(3)若min{2x﹣5,x+3}=﹣2,求x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com