
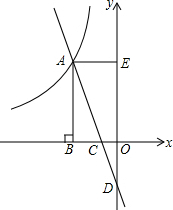
 如图,直线y=kx-2与双曲线y=-$\frac{6}{x}$(x<0)交于点A,与x轴交于点C,与y轴交于点D.AB⊥x轴于点B,AE⊥y轴于点E,△ABC的面积为2.
如图,直线y=kx-2与双曲线y=-$\frac{6}{x}$(x<0)交于点A,与x轴交于点C,与y轴交于点D.AB⊥x轴于点B,AE⊥y轴于点E,△ABC的面积为2.分析 (1)根据反比例函数系数k的几何意义即可求得;
(2)设A(x,-$\frac{6}{x}$),根据△ABC的面积为2,求得BC=-$\frac{2}{3}$x,OC=-$\frac{1}{3}$x,根据△ABC∽△DOC求得$\frac{AB}{OD}$=$\frac{BC}{OC}$=$\frac{2}{1}$,由直线的解析式求得D的坐标为(0,-2)得出OD=2,从而求得AB=4,代入反比例函数解析式求得A的坐标,求得OB的长,即可求得C的坐标.
解答 解:(1)∵双曲线为y=-$\frac{6}{x}$(x<0),
∴四边形ABOE的面积为6,
∵△ABC的面积为2.
∴四边形OCAE的面积为4.
(2)∵A点是双曲线y=-$\frac{6}{x}$(x<0)上的点,
设A(x,-$\frac{6}{x}$),
∴AB=-$\frac{6}{x}$,
∵△ABC的面积为2.
∴$\frac{1}{2}$AB•BC=2,即$\frac{1}{2}$×(-$\frac{6}{x}$)•BC=2
∴BC=-$\frac{2}{3}$x,
∴OC=-$\frac{1}{3}$x,
∵AB⊥x轴于点B,
∴AB∥y轴,
∴△ABC∽△DOC,
∴$\frac{AB}{OD}$=$\frac{BC}{OC}$=$\frac{-\frac{2}{3}x}{-\frac{1}{3}x}$=$\frac{2}{1}$,
由直线y=kx-2可知D(0,-2),
∴OD=2,
∴AB=4,
∴-$\frac{6}{x}$=4,解得x=-$\frac{3}{2}$,
∴A(-$\frac{3}{2}$,4),
代入y=kx-2得,4=-$\frac{3}{2}$k-2,解得k=-4,
∴直线:y=-4x-2,
令y=0,则x=-$\frac{1}{2}$,
∴C(-$\frac{1}{2}$,0).
点评 本题考查了反比例函数和一次函数的交点问题,三角形相似的判定和性质,待定系数法求解析式,求得A的坐标是解题的关键.


科目:初中数学 来源: 题型:解答题
 兰新铁路的通车,圆了全国人民的一个梦,坐上火车去观赏青海门源百里油菜花海,感受大美青海独特的高原风光,暑假某校准备组织学生、老师到门源进行社会实践,为了便于管理,师生必须乘坐在同一列高铁上,根据报名人数,若都买一等座单程火车票需2340元,若都买二等座单程火车票花钱最少,则需1650元:
兰新铁路的通车,圆了全国人民的一个梦,坐上火车去观赏青海门源百里油菜花海,感受大美青海独特的高原风光,暑假某校准备组织学生、老师到门源进行社会实践,为了便于管理,师生必须乘坐在同一列高铁上,根据报名人数,若都买一等座单程火车票需2340元,若都买二等座单程火车票花钱最少,则需1650元:| 运行区间 | 票价 | ||
| 上车站 | 下车站 | 一等座 | 二等座 |
| 西宁 | 门源 | 36元 | 30元 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
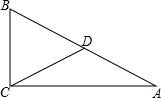 如图,已知在Rt△ABC中,D是斜边AB的中点,AC=4,BC=2,将△ACD沿直线CD折叠,点A落在点E处,联结AE,那么线段AE的长度等于$\frac{8\sqrt{5}}{5}$.
如图,已知在Rt△ABC中,D是斜边AB的中点,AC=4,BC=2,将△ACD沿直线CD折叠,点A落在点E处,联结AE,那么线段AE的长度等于$\frac{8\sqrt{5}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
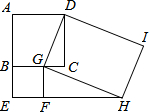 正方形ABCD、BEFG和矩形DGHI的位置如图,其中G、F两点分别在BC、EH上.若AB=5,BG=3,则△GFH的面积为$\frac{45}{4}$.
正方形ABCD、BEFG和矩形DGHI的位置如图,其中G、F两点分别在BC、EH上.若AB=5,BG=3,则△GFH的面积为$\frac{45}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
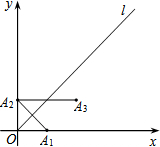 如图,在平面直角坐标系xOy中,函数y=x的图象为直线l,作点A1(1,0)关于直线l的对称点A2,将A2向右平移2个单位得到点A3;再作A3关于直线l的对称点A4,将A4向右平移2个单位得到点A5;….则按此规律,所作出的点A2015的坐标为( )
如图,在平面直角坐标系xOy中,函数y=x的图象为直线l,作点A1(1,0)关于直线l的对称点A2,将A2向右平移2个单位得到点A3;再作A3关于直线l的对称点A4,将A4向右平移2个单位得到点A5;….则按此规律,所作出的点A2015的坐标为( )| A. | (1007,1008) | B. | (1008,1007) | C. | (1006,1007) | D. | (1007,1006) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
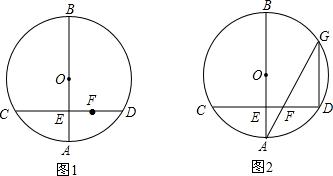
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
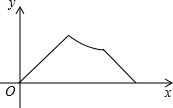 已知点A为某封闭图形边界上一定点,动点P从点A出发,沿其边界逆时针匀速运动一周.设点P运动的时间为x,线段AP的长为y.表示y与x的函数关系的图象大致如图,则该封闭图形可能是( )
已知点A为某封闭图形边界上一定点,动点P从点A出发,沿其边界逆时针匀速运动一周.设点P运动的时间为x,线段AP的长为y.表示y与x的函数关系的图象大致如图,则该封闭图形可能是( )| A. | 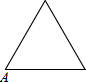 | B. | 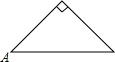 | C. | 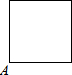 | D. | 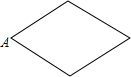 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com