
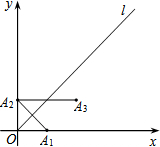
 如图,在平面直角坐标系xOy中,函数y=x的图象为直线l,作点A1(1,0)关于直线l的对称点A2,将A2向右平移2个单位得到点A3;再作A3关于直线l的对称点A4,将A4向右平移2个单位得到点A5;….则按此规律,所作出的点A2015的坐标为( )
如图,在平面直角坐标系xOy中,函数y=x的图象为直线l,作点A1(1,0)关于直线l的对称点A2,将A2向右平移2个单位得到点A3;再作A3关于直线l的对称点A4,将A4向右平移2个单位得到点A5;….则按此规律,所作出的点A2015的坐标为( )| A. | (1007,1008) | B. | (1008,1007) | C. | (1006,1007) | D. | (1007,1006) |
科目:初中数学 来源: 题型:填空题
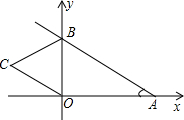 如图,直线y=kx+4与x,y轴分别交于A,B两点,以OB为边在y轴左侧作等边三角形OBC,将△OBCB沿y轴翻折后,点C的对应点C′恰好落在直线AB上,则k的值为-$\frac{\sqrt{3}}{3}$.
如图,直线y=kx+4与x,y轴分别交于A,B两点,以OB为边在y轴左侧作等边三角形OBC,将△OBCB沿y轴翻折后,点C的对应点C′恰好落在直线AB上,则k的值为-$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
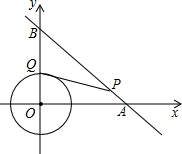 如图,⊙O是以原点为圆心,$\sqrt{2}$为半径的圆,点P是直线y=-x+6上的一点,过点P 作⊙O的一条切线PQ,Q为切点,则△OPQ面积的最小值为2$\sqrt{2}$.
如图,⊙O是以原点为圆心,$\sqrt{2}$为半径的圆,点P是直线y=-x+6上的一点,过点P 作⊙O的一条切线PQ,Q为切点,则△OPQ面积的最小值为2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
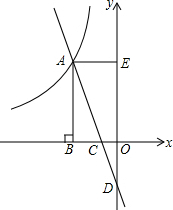 如图,直线y=kx-2与双曲线y=-$\frac{6}{x}$(x<0)交于点A,与x轴交于点C,与y轴交于点D.AB⊥x轴于点B,AE⊥y轴于点E,△ABC的面积为2.
如图,直线y=kx-2与双曲线y=-$\frac{6}{x}$(x<0)交于点A,与x轴交于点C,与y轴交于点D.AB⊥x轴于点B,AE⊥y轴于点E,△ABC的面积为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
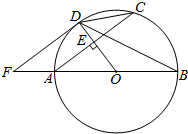 如图,AB是⊙O的直径.半径OD垂直弦AC于点E.F是BA延长线上一点,∠CDB=∠BFD.
如图,AB是⊙O的直径.半径OD垂直弦AC于点E.F是BA延长线上一点,∠CDB=∠BFD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
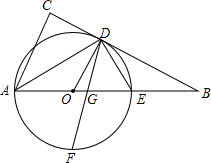 如图,E是△ABC的边AB上一点,以AE为直径的⊙O经过BC上的一点D,且OD∥AC,∠ADE的平分线DF交AB于G,交⊙O于F,且BD=BG
如图,E是△ABC的边AB上一点,以AE为直径的⊙O经过BC上的一点D,且OD∥AC,∠ADE的平分线DF交AB于G,交⊙O于F,且BD=BG查看答案和解析>>
科目:初中数学 来源: 题型:解答题
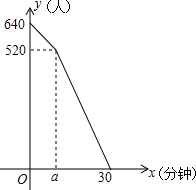 汛期来临,水库水位不断上涨,经勘测发现,水库现在超过警戒线水量640万米3,设水流入水库的速度是固定的,每个泄洪闸速度也是固定的,泄洪时,每小时流入水库的水量16万米3,每小时每个泄洪闸泄洪14万米3,已知泄洪的前a小时只打开了两个泄洪闸,水库超过警戒线的水量y(万米3)与泄洪时间s(小时)的关系如图所示,根据图象解答问题:
汛期来临,水库水位不断上涨,经勘测发现,水库现在超过警戒线水量640万米3,设水流入水库的速度是固定的,每个泄洪闸速度也是固定的,泄洪时,每小时流入水库的水量16万米3,每小时每个泄洪闸泄洪14万米3,已知泄洪的前a小时只打开了两个泄洪闸,水库超过警戒线的水量y(万米3)与泄洪时间s(小时)的关系如图所示,根据图象解答问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
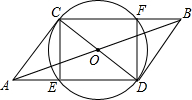 如图:CD是⊙O的直径,线段AB过圆心O,且OA=OB=$\sqrt{5}$,CD=2,连接AC、AD、BD、BC、AD、CB分别交⊙O于E、F.
如图:CD是⊙O的直径,线段AB过圆心O,且OA=OB=$\sqrt{5}$,CD=2,连接AC、AD、BD、BC、AD、CB分别交⊙O于E、F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com