
为了举行班级晚会,孔明准备去商店购买20乒乓球做道具,并买一些乒乓球拍做奖品,已知乒乓球每个1.5元,球拍每个22元,如果购买金额不超过200元,且买的球拍尽可能多,那么孔明应该买多少个球拍?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
已知:如图,点A(3,4)在直线y=kx上,过A作AB⊥x轴于点B.
(1)求k的值;
(2)设点B关于直线y=kx的对称点为C点,求ΔABC外接圆的面积;
|
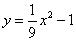 与x轴的交点为Q,试问在直线y=kx上是否存在点P,使得
与x轴的交点为Q,试问在直线y=kx上是否存在点P,使得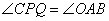 ,如果存在,请求出P点的坐标;如果不存在,请说明理由.
,如果存在,请求出P点的坐标;如果不存在,请说明理由. 查看答案和解析>>
科目:初中数学 来源: 题型:
一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量 (单位:升)与时间
(单位:升)与时间 (单位:分)之间的部分关系如图所示.那么,从关闭进水管起 分钟该容器内的水恰好放完。
(单位:分)之间的部分关系如图所示.那么,从关闭进水管起 分钟该容器内的水恰好放完。

查看答案和解析>>
科目:初中数学 来源: 题型:
已知抛物线的表达式为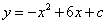
(1)若抛物线与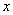 轴有交点,求
轴有交点,求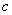 的取值范围;
的取值范围;
(2)设抛物线与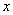 轴两个交点的横坐标分别为
轴两个交点的横坐标分别为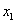 、
、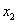 ,若
,若 ,求
,求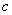 的值;
的值;
(3)若P、Q是抛物线上位于第一象限的不同两点,PA、QB都垂直于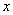 轴,垂足分别为A、B,且△OPA与△OQB全等,求证:
轴,垂足分别为A、B,且△OPA与△OQB全等,求证: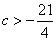
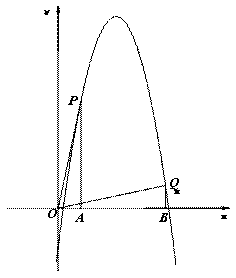
查看答案和解析>>
科目:初中数学 来源: 题型:
.我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,AF,BE是△ABC的中线, AF⊥BE , 垂足为P.像△ABC这样的三角形均为“中垂三角形”.设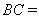
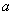 ,
,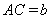 ,
,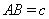 .
.
特例探索
(1)如图1,当∠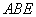 =45°,
=45°,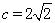 时,
时, = ,
= , ;
;
如图2,当∠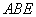 =30°,
=30°,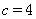 时,
时, 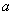 = ,
= ,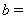 ;
;

归纳证明
(2)请你观察(1)中的计算结果,猜想 三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式;
三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式;
拓展应用
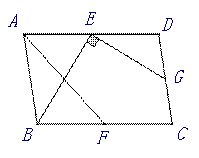
(3)如图4,在□ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG, AD= 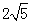 ,AB=3.
,AB=3.
求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com