
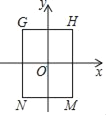
【题目】对于点P(a,b),点Q(c,d),如果a﹣b=c﹣d,那么点P与点Q就叫作等差点.例如:点P(4,2),点Q(﹣1,﹣3),因4﹣2=1﹣(﹣3)=2,则点P与点Q就是等差点.如图在矩形GHMN中,点H(2,3),点N(﹣2,﹣3),MN⊥y轴,HM⊥x轴,点P是直线y=x+b上的任意一点(点P不在矩形的边上),若矩形GHMN的边上存在两个点与点P是等差点,则b的取值范围为_____.
科目:初中数学 来源: 题型:
【题目】如图,直线 ![]() ∥
∥ ![]() ∥
∥ ![]() ,且
,且 ![]() 与
与 ![]() 的距离为1,
的距离为1, ![]() 与
与 ![]() 的距离为2,等腰 △ABC的顶点分别在直线
的距离为2,等腰 △ABC的顶点分别在直线 ![]() ,
, ![]() ,
, ![]() 上,AB=AC,∠BAC=120° ,则等腰三角形的底边长为。
上,AB=AC,∠BAC=120° ,则等腰三角形的底边长为。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,![]() 、
、![]() 是直线,
是直线,![]() ,
,![]() ,
,![]() .
.![]() 与
与![]() 平行吗?为什么?
平行吗?为什么?

解:![]() ,理由如下:
,理由如下:
∵![]() (已知)
(已知)
∴![]() ( )
( )
∵![]() (已知)
(已知)
∴![]() _________( )
_________( )
∵![]() (已知)
(已知)
∴![]() ( )
( )
即![]()
∴![]() _________(等量代换)
_________(等量代换)
∴![]() ( )
( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“低碳生活,绿色出行”理念的普及,新能源汽车正逐渐成为人们喜爱的交通工具.某汽车销售公司计划购进一批新能源汽车尝试进行销售,据了解2辆A型汽车、3辆B型汽气车的进价共计80万元;3辆A型汽车、2辆B型汽车的进价共计95万元。
(1)求A、B两种型号的汽车每辆进价分别为多少方元?
(2)若该公司计划正好用200万元购进以上两种型号的新能源汽车(两种型号的汽车均购买),请你帮助该公司设计购买方案;
(3)若该汽车销售公司销售1辆A型汽车可获利8000元,销售1辆B型汽车可获利5000元,在(2)中的购买方案中,假如这些新能源汽车全部售出,哪种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(1,2),解答以下问题:
(1)请在图中建立适当的直角坐标系,并写出图书馆B位置的坐标;

(2)若体育馆位置坐标为C(-3,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形![]() 中,
中,![]() 为对角线
为对角线![]() 上一点,且
上一点,且![]() ,
,![]() 交
交![]() 于
于![]() ,延长
,延长![]() 交
交![]() 于
于![]() .
.
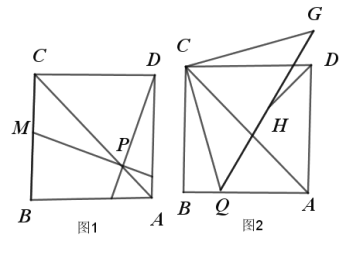
(1)求证:![]() ;
;
(2)已知如图(2),![]() 为
为![]() 上一点,连接
上一点,连接![]() ,并将
,并将![]() 逆时针旋转
逆时针旋转![]() 至
至![]() ,连接
,连接![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() ,试求出
,试求出![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列一段文字,再解答问题
已知在平面内有两点![]() ,
,![]() ,其两点间的距离公式为
,其两点间的距离公式为![]() ,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为
,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为![]() 或
或![]()
![]() 已知点
已知点![]() ,
,![]() ,试求A,B两点间的距离;
,试求A,B两点间的距离;![]() 已知点A,B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为
已知点A,B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为![]() ,试求A,B两点间的距离;
,试求A,B两点间的距离;![]() 已知点
已知点![]() ,
,![]() ,判断线段AB,BC,AC中哪两条是相等的?并说明理由.
,判断线段AB,BC,AC中哪两条是相等的?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形中有大小不同的平行四边形,第一幅图中有1个平行四边形,第二幅图中有3个平行四边形,第三幅图中有5个平行四边形,则第6幅和第7幅图中合计有( )个平行四边形
![]()
A.22B.24C.26D.28
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索题:图a是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图b的形状拼成一个正方形.

(1)请用两种不同的方法,求图b中阴影部分的面积:
方法1: ; 方法2: ;
(2)观察图b,写出代数式![]() ,
, ![]() ,
, ![]() 之间的等量关系,并通过计算验证;
之间的等量关系,并通过计算验证;
(3)根据(2)题中的等量关系,解决如下问题:若![]() ,
, ![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com