练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知，如图，、是直线，，，.与平行吗？为什么？

    解：，理由如下：

    ∵（已知）

    ∴（ ）

    ∵（已知）

    ∴_________（ ）

    ∵（已知）

    ∴（ ）

    即

    ∴_________（等量代换）

    ∴（ ）

    【答案】两直线平行，同位角相等；∠BAE；等量代换；等式的性质；∠DAC；内错角相等，两直线平行．

    【解析】

    由平行线的性质可得，进而可得，而由易得，从而可得∠DAC，再根据平行线的判定即得结论．

    解：，理由如下：

    ∵（已知），

    ∴（两直线平行，同位角相等），

    ∵（已知），

    ∴（等量代换），

    ∵（已知），

    ∴（等式的性质），

    即．

    ∴∠DAC （等量代换），

    ∴（内错角相等，两直线平行）．

    故答案为：两直线平行，同位角相等；；等量代换；等式的性质；∠DAC；内错角相等，两直线平行．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，AF∥CD，CB平分∠ACD，BD平分∠EBF，且BC⊥BD，下列结论：① BC平分∠ABE；② AC∥BE；③ ∠CBE+∠D＝90°；④ ∠DEB＝2∠ABC．其中正确结论的个数有（　　）

    A.1个B.2个C.3个D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解方程：

    （1）4－x＝3(2－x)

    （2） =1

    （3）

    （4）

    （5）

    （6）4x﹣5=．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线y=x+m与反比例函数 相交于点A（6，2），与x轴交于B点，点C在直线AB上且 ．过B、C分别作y轴的平行线交双曲线 于D、E两点．

    （1）求m、k的值；
    （2）求点D、E坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，顶点为（2，﹣1）的抛物线交y轴于A点，交x轴于B、C两点（点B在点C的左侧），已知A点坐标为（0，3），连接AB．

    （1）求此抛物线的解析式；
    （2）过点B作线段AB的垂线交抛物线于点D，如果以点C为圆心的圆与直线BD相切，请判断抛物线的对称轴l与⊙C有怎样的位置关系，并给出证明；
    （3）已知点P是抛物线上的一个动点，且位于A，C两点之间，问：当点P运动到什么位置时，△PAC的面积最大？并求出此时P点的坐标和△PAC的最大面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于一个图形，通过两种不同的方法计算它的面积，可以得到一个数学等式，例如图1可以得到，请解答下列问题：

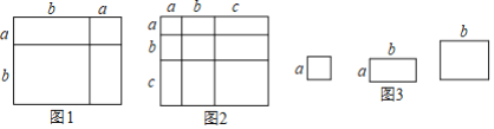
    （1）写出图2中所表示的数学等式____________________________________

    （2）根据整式乘法的运算法则，通过计算验证上述等式.

    （3）利用（1）中得到的结论，解决下面的问题：

    若，，则_________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两人相约元旦登山，甲、乙两人距地面的高度y(m)与登山时间x(min)之间的函数图像如图所示，根据图像所提供的信息解答下列问题：

    （1）t= min.

    （2）若乙提速后，乙登山的上升速度是甲登山的上升速度3倍，

    ①则甲登山的的上升速度是 m/min；

    ②请求出甲登山过程中，距地面的高度y(m)与登山时间x(min)之间的函数关系式.

    ③当甲、乙两人距地面高度差为70m时，求x的值（直接写出满足条件的x值）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

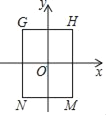
    【题目】对于点P（a，b），点Q（c，d），如果a﹣b＝c﹣d，那么点P与点Q就叫作等差点．例如：点P（4，2），点Q（﹣1，﹣3），因4﹣2＝1﹣（﹣3）＝2，则点P与点Q就是等差点．如图在矩形GHMN中，点H（2，3），点N（﹣2，﹣3），MN⊥y轴，HM⊥x轴，点P是直线y＝x+b上的任意一点（点P不在矩形的边上），若矩形GHMN的边上存在两个点与点P是等差点，则b的取值范围为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB∥CD，分别探讨下面四个图形中∠APC与∠PAB、∠PCD的关系，请你从所得到的关系中任选一个加以说明。（适当添加辅助线，其实并不难）

    (1) (2) (3) (4)

    查看答案和解析>>

    同步练习册答案