
【题目】如图,直线y=x+m与反比例函数 ![]() 相交于点A(6,2),与x轴交于B点,点C在直线AB上且
相交于点A(6,2),与x轴交于B点,点C在直线AB上且 ![]() .过B、C分别作y轴的平行线交双曲线
.过B、C分别作y轴的平行线交双曲线 ![]() 于D、E两点.
于D、E两点.
(1)求m、k的值;
(2)求点D、E坐标.
【答案】
(1)解:把A(6,2)代入y=x+m与y= ![]() ,得
,得
m=﹣4,k=12
(2)解:过A作AM⊥x轴于M,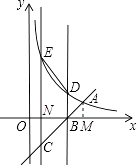
由(1)可得,直线解析式为y=x﹣4,y= ![]() ,
,
当y=0时,x﹣4=0,x=4,
∴B(4,0),
∴BM=2,
当x=4时,y= ![]() =3,
=3,
∴D(4,3).
又 ![]() =
= ![]() ,
,
∴BN=3,
∴点C的横坐标是1,
又直线AB的解析式是y=x﹣4,
∴点C的纵坐标是﹣3,
又CE∥y轴,
∴点E的横坐标是1,
再根据反比例函数的解析式求得点E的纵坐标是12,
则E(1,12).
【解析】(1)利用待定系数法,把A(6,2)分别代入解析式,可求出解析式;(2)利用解析式和成比例线段的性质,可求出D、E的横坐标,进而求出纵坐标.


科目:初中数学 来源: 题型:
【题目】如图所示,O是矩形ABCD的对角线的交点,DE∥AC,CE∥BD.
(1)求证:OE⊥DC.
(2)若∠AOD=120°,DE=2,求矩形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线 ![]() ∥
∥ ![]() ∥
∥ ![]() ,且
,且 ![]() 与
与 ![]() 的距离为1,
的距离为1, ![]() 与
与 ![]() 的距离为2,等腰 △ABC的顶点分别在直线
的距离为2,等腰 △ABC的顶点分别在直线 ![]() ,
, ![]() ,
, ![]() 上,AB=AC,∠BAC=120° ,则等腰三角形的底边长为。
上,AB=AC,∠BAC=120° ,则等腰三角形的底边长为。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣2x2﹣8x﹣6与x轴交于点A,B,把抛物线在x轴及其上方的部分记作C1 , 将C1向左平移得C2 , C2与x轴交于点B,D.若直线y=﹣x+m与C1 , C2共有3个不同的交点,则m的取值范围是( )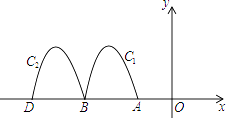
A.﹣3<m<﹣ ![]()
B.![]()
C.﹣2<m< ![]()
D.﹣3<m<﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从-2,-1,0,1,2,3,5这七个数中,随机抽取一个数记为m,若数m使关于x的不等式组![]() 无解,且使关于x的一元一次方程(m-2)x=3有整数解,那么这六个数所有满足条件的m的个数有( )
无解,且使关于x的一元一次方程(m-2)x=3有整数解,那么这六个数所有满足条件的m的个数有( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整:收集数据:从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分)如下:
甲 | 78 | 86 | 74 | 81 | 75 | 76 | 87 | 70 | 75 | 90 |
75 | 79 | 81 | 70 | 74 | 80 | 86 | 69 | 83 | 77 | |
乙 | 93 | 73 | 88 | 81 | 72 | 81 | 94 | 83 | 77 | 83 |
80 | 81 | 70 | 81 | 73 | 78 | 82 | 80 | 70 | 40 |
(1)整理、描述数据:按如分数段整理、描述这两组样本数据(请补全表格):
|
|
|
|
|
| |
甲 | 0 | 0 | 1 | 11 | 7 | 1 |
乙 | __________ | 0 | 0 | __________ | __________ | __________ |
(说明:成绩80分及以上为生产技能优秀,70-79分为生产技能良好,60-69分为生产技能合格,60分以下为生产技能不合格)
分析数据:两组样本数据的平均数、中位数、众数如表所示(请补全表格):
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.3 | __________ | 75 |
乙 | 78 | 80.5 | __________ |
得出结论:
(2)估计乙部门生产技能优秀的员工人数为__________;
(3)你认为__________部门员工的生产技能水平较高,说明理由(至少从两个不同的角度说明推断的合理性).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,![]() 、
、![]() 是直线,
是直线,![]() ,
,![]() ,
,![]() .
.![]() 与
与![]() 平行吗?为什么?
平行吗?为什么?

解:![]() ,理由如下:
,理由如下:
∵![]() (已知)
(已知)
∴![]() ( )
( )
∵![]() (已知)
(已知)
∴![]() _________( )
_________( )
∵![]() (已知)
(已知)
∴![]() ( )
( )
即![]()
∴![]() _________(等量代换)
_________(等量代换)
∴![]() ( )
( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“低碳生活,绿色出行”理念的普及,新能源汽车正逐渐成为人们喜爱的交通工具.某汽车销售公司计划购进一批新能源汽车尝试进行销售,据了解2辆A型汽车、3辆B型汽气车的进价共计80万元;3辆A型汽车、2辆B型汽车的进价共计95万元。
(1)求A、B两种型号的汽车每辆进价分别为多少方元?
(2)若该公司计划正好用200万元购进以上两种型号的新能源汽车(两种型号的汽车均购买),请你帮助该公司设计购买方案;
(3)若该汽车销售公司销售1辆A型汽车可获利8000元,销售1辆B型汽车可获利5000元,在(2)中的购买方案中,假如这些新能源汽车全部售出,哪种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形中有大小不同的平行四边形,第一幅图中有1个平行四边形,第二幅图中有3个平行四边形,第三幅图中有5个平行四边形,则第6幅和第7幅图中合计有( )个平行四边形
![]()
A.22B.24C.26D.28
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com