
 已知:O是坐标原点,P(m,n)(m>0)是函数y=$\frac{k}{x}$(k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+$\frac{{n}^{4}}{4}$.
已知:O是坐标原点,P(m,n)(m>0)是函数y=$\frac{k}{x}$(k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+$\frac{{n}^{4}}{4}$.分析 (1)根据三角形的面积公式得到s=$\frac{1}{2}$a•n.而s=1+$\frac{{n}^{4}}{4}$,把n=1代入就可以得到a的值.
(2)易证△OPA是等腰直角三角形,得到m=n=$\frac{a}{2}$,根据三角形的面积S=$\frac{1}{2}$•an,就可以解得k的值.
(3)易证△OPQ∽△OAP,根据相似三角形面积的比等于相似比的平方,就可以得到关于k,n的方程,从而求出k,n的值,得到OP的值
解答 解:过点P作PQ⊥x轴于Q,则PQ=n,OQ=m,
(1)当n=1时,s=$\frac{5}{4}$,
∵s=$\frac{1}{2}$an,
∴a=$\frac{2s}{n}$=$\frac{5}{2}$,
∴点A坐标($\frac{5}{2}$,0).
(2)∵OP=AP,PA⊥OP,
∴△OPA是等腰直角三角形.
∴m=n=$\frac{a}{2}$,
∴$\frac{1}{2}$•a•n=1+$\frac{{n}^{4}}{4}$,
即n4-4n2+4=0,∵k=n2,
∴k2-4k+4=0,
∴k=2.
(3)由s=1+$\frac{{n}^{4}}{4}$=$\frac{1}{2}$an,整理得a=$\frac{2}{n}$+$\frac{{n}^{3}}{2}$,
∵PA⊥OP,作PQ⊥OA于Q,∴△OPQ∽△OAP.
∴OP2=OQ•OA,∵OP2=m2+n2,又m=$\frac{k}{n}$,
∴$\frac{k}{n}$•a=$\frac{{k}^{2}}{{n}^{2}}$+n2,
化简得:2n4+2k2-kn4-4k=0 即(k-2)(2k-n4)=0,
∴k=2或k=$\frac{{n}^{4}}{2}$,
∵k≠$\frac{{n}^{4}}{2}$,
∴k=2,
∵OP2=m2+n2=$\frac{4}{{n}^{2}}$+n2,且n是大于0且小于20的整数,
当n=1时,OP2=5,
当n=2时,OP2=5,
当n=3时,OP2=32+$\frac{4}{{3}^{2}}$>32,
当n是大于3且小于20的整数时,显然有OP2>5,
∴OP2的最小值是5.
点评 本题考查反比例函数综合题、一次函数、等腰直角三角形的性质、勾股定理、相似三角形等知识,解题的关键是用转化的思想,把问题转化为方程去思考,属于中考比较难的题目.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
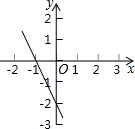 如图,是函数y=kx+b的图象,当y<-1时,x的取值范围是( )
如图,是函数y=kx+b的图象,当y<-1时,x的取值范围是( )| A. | x<-$\frac{1}{2}$ | B. | x>-$\frac{1}{2}$ | C. | x<-$\frac{1}{4}$ | D. | x>-$\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在直角坐标系中,我们把横、纵坐标都是整数的点叫做整点.且规定,正方形的内部不包含边界上的点.观察如图所示的中心在原点、一边平行于x轴的正方形:边长为1的正方形内部有1个整点,边长为2的正方形内部有1个整点,边长为3的正方形内部有9个整点,…,则边长为8的正方形内部的整点的个数为49.
在直角坐标系中,我们把横、纵坐标都是整数的点叫做整点.且规定,正方形的内部不包含边界上的点.观察如图所示的中心在原点、一边平行于x轴的正方形:边长为1的正方形内部有1个整点,边长为2的正方形内部有1个整点,边长为3的正方形内部有9个整点,…,则边长为8的正方形内部的整点的个数为49.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
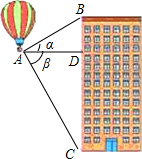 热气球的探测器显示,从热气球看一栋楼顶部的仰角α为27°,看这栋楼底部的俯角β为58°,热气球与这栋楼的水平距离为120米,这栋楼有多高(结果取整数)?
热气球的探测器显示,从热气球看一栋楼顶部的仰角α为27°,看这栋楼底部的俯角β为58°,热气球与这栋楼的水平距离为120米,这栋楼有多高(结果取整数)?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com