
分析 根据y随x的增大而增大可得2k-3>0,再由一次函数与y轴的交点在x轴的上方,可得:2-k>0,联立求解即可.
解答 解:∵y随x的增大而增大,
∴2k-3>0,
解得:k>$\frac{3}{2}$,
又∵一次函数与y轴的交点在x轴的上方,
∴2-k>0,
解得:k<2.
综上可得:$\frac{3}{2}$<k<2.
故答案为:$\frac{3}{2}$<k<2.
点评 本题考查了一次函数的性质,解答本题的关键是掌握:
①k>0,y随x的增大而增大,函数从左到右上升;k<0,y随x的增大而减小;
②y=kx+b与y轴交于(0,b),当b>0时,(0,b)在y轴的正半轴上,直线与y轴交于正半轴;当b<0时,(0,b)在y轴的负半轴,直线与y轴交于负半轴.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
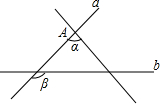 如图,直线a与直线c的夹角是∠α,直线b与直线c的夹角是∠β,把直线a“绕”点A按逆时针方向旋转,当∠α与∠β满足∠α=∠β时,直线a∥b,理由是同位角相等,两直线平行.
如图,直线a与直线c的夹角是∠α,直线b与直线c的夹角是∠β,把直线a“绕”点A按逆时针方向旋转,当∠α与∠β满足∠α=∠β时,直线a∥b,理由是同位角相等,两直线平行.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 企业的工业废料处理有两种方式,一种是运送到垃圾厂进行集中处理,另一种是通过企业的自身设备进行处理.某企业去年每月的工业废料均为120吨,由于垃圾厂处于调试阶段,处理能力有限,该企业采取两种处理方式同时进行.
企业的工业废料处理有两种方式,一种是运送到垃圾厂进行集中处理,另一种是通过企业的自身设备进行处理.某企业去年每月的工业废料均为120吨,由于垃圾厂处于调试阶段,处理能力有限,该企业采取两种处理方式同时进行.| 月份x(月) | 1 | 2 | 3 | 4 | 5 | 6 |
| 运送的工业废料y1(吨) | 120 | 60 | 40 | 30 | 24 | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系中,等腰直角三角形ABC的直角顶点A的坐标为(2,0),顶点B的坐标为(0,1),顶点C在第一象限,若函数y=$\frac{k}{x}$(x>0)的图象经过点C,则k的值为( )
如图,在平面直角坐标系中,等腰直角三角形ABC的直角顶点A的坐标为(2,0),顶点B的坐标为(0,1),顶点C在第一象限,若函数y=$\frac{k}{x}$(x>0)的图象经过点C,则k的值为( )| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:O是坐标原点,P(m,n)(m>0)是函数y=$\frac{k}{x}$(k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+$\frac{{n}^{4}}{4}$.
已知:O是坐标原点,P(m,n)(m>0)是函数y=$\frac{k}{x}$(k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+$\frac{{n}^{4}}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com