
 已知点D是△ABC内一定点,且有∠DAC=∠DCB=∠DBA=30°,求证:△ABC是等边三角形.
已知点D是△ABC内一定点,且有∠DAC=∠DCB=∠DBA=30°,求证:△ABC是等边三角形. 分析 由已知推导出△ABC不一定是等边三角形.法一:举出反例;法二:以C为原点,CD为x轴建立直角坐标系,设D(1,0),B($\frac{\sqrt{3}a}{2}$,$\frac{a}{2}$),A(x,y),推导出当BC=a=$\sqrt{3}$时命题成立.可见,此命题是假命题.
解答  证明:△ABC不一定是等边三角形.
证明:△ABC不一定是等边三角形.
证法一:如图所示的三角形存在,但它不是等边三角形,故△ABC不一定是等边三角形.
证法二:以C为原点,CD为x轴建立直角坐标系,设D(1,0),B($\frac{\sqrt{3}a}{2}$,$\frac{a}{2}$),A(x,y),
则BD斜率k1=$\frac{\frac{a}{2}}{\frac{\sqrt{3}}{2}a-1}$=$\frac{a}{\sqrt{3}a-2}$,AB斜率k2=$\frac{a-2y}{\sqrt{3}a-2x}$,
AC斜率k3=$\frac{y}{x}$,AD斜率k4=$\frac{y}{x-1}$,
其中a>$\frac{2}{\sqrt{3}}$,x>0>y,
由∠DAC=∠DBA=30°及到角公式得:
$\frac{{k}_{2}-{k}_{1}}{1+{k}_{2}{k}_{1}}$=$\frac{\frac{a-2y}{\sqrt{3}a-2x}-\frac{a}{\sqrt{3}a-2}}{1+\frac{a-2y}{\sqrt{3}a-2x}•\frac{a}{\sqrt{3}a-2}}$=$\frac{1}{\sqrt{3}}$.
∴$\sqrt{3}$[(a-2y)($\sqrt{3}$a3-2)-a($\sqrt{3}$a-2x)]=($\sqrt{3}$a-2)($\sqrt{3}$a-2x)+a(a-2y),
$\sqrt{3}$[-2a+(4-2$\sqrt{3}$a)y+2ax]=4a2-2$\sqrt{3}$a+(4-2$\sqrt{3}$a)x-2ay,
(4$\sqrt{3}$-6a)y+2$\sqrt{3}$ax=4a2+(4-2$\sqrt{3}$a)x-2ay,
(4$\sqrt{3}$-4a)y=(4-4a$\sqrt{3}$)x+4a2,
y=$\frac{(1-\sqrt{3}a)x+{a}^{2}}{\sqrt{3}-a}$,①
$\frac{{k}_{3}-{k}_{4}}{1+{k}_{3}{k}_{4}}$=$\frac{\frac{y}{x}-\frac{y}{x-1}}{1+\frac{{y}^{2}}{{x}^{2}-x}}$=$\frac{1}{\sqrt{3}}$,
x2-x+y2+$\sqrt{3}$y=0,②
由①、②解出x,y.
把①代入②,x2-x+$\frac{(1-\sqrt{3}a)x+{a}^{2}}{\sqrt{3}-a}$•[$\frac{(1-\sqrt{3}a)x+{a}^{2}}{\sqrt{3}-a}$+$\sqrt{3}$]=0,
(x2-x)($\sqrt{3}$-a)2+[(1-$\sqrt{3}$a)x+a2][(1-$\sqrt{3}$a)x+a2+3-$\sqrt{3}$a]=0,
(x2-x)(3-2$\sqrt{3}$a+a2)+(1-$\sqrt{3}$a)2x2+(1-$\sqrt{3}$a)(2a2-$\sqrt{3}$a+3)x+a4-$\sqrt{3}$3a3+3a2=0,
(4a2-4$\sqrt{3}$a+4)x2+(-2$\sqrt{3}$a3+4a2-2$\sqrt{3}$a)x+a4-$\sqrt{3}$a3+3a2=0,③
若△ABC是等边三角形,则③的根是$\frac{\sqrt{3}a}{2}$,
把x=$\frac{\sqrt{3}a}{2}$代入③,得
3a4-3$\sqrt{3}$a3+3a2-3a4+2$\sqrt{3}$a3-3a2+a4-$\sqrt{3}$a3+3a2
=a4-2$\sqrt{3}$a3+3a2=a2(a-$\sqrt{3}$)2=0,
仅当BC=a=$\sqrt{3}$时命题成立.可见,此命题是假命题.
故△ABC不一定是等边三角形.
点评 本题考查等边三角形的证明,在判断一个命题是假命题时,举出一个反例即可.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
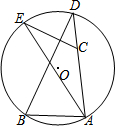 如图,△ABD内接于⊙O,点C在线段AD上,AC=2CD,点E在$\widehat{BD}$上,∠ECD=∠ABD,EC=1,则AE等于( )
如图,△ABD内接于⊙O,点C在线段AD上,AC=2CD,点E在$\widehat{BD}$上,∠ECD=∠ABD,EC=1,则AE等于( )| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
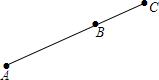 如图,A、B、C是一条公路边的三个连锁超市,且A、B、C在一条直线上,计划在A、C之间的公路边建一个配货中心P,负责向3个超市送货.
如图,A、B、C是一条公路边的三个连锁超市,且A、B、C在一条直线上,计划在A、C之间的公路边建一个配货中心P,负责向3个超市送货.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
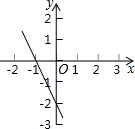 如图,是函数y=kx+b的图象,当y<-1时,x的取值范围是( )
如图,是函数y=kx+b的图象,当y<-1时,x的取值范围是( )| A. | x<-$\frac{1}{2}$ | B. | x>-$\frac{1}{2}$ | C. | x<-$\frac{1}{4}$ | D. | x>-$\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com