
【题目】我市要开展“不忘初心,牢记使命”主题演讲比,某中学将参加本校选拔赛的50名选手的成绩(满分为100分,得分为正整数)分成五组,并绘制了不完整的统计图表.
分数段 | 频数 | 频率 |
69.5~75.5 | 9 | 0.18 |
75.5~81.5 | m | 0.16 |
81.5~87.5 | 14 | 0.28 |
87.5~93.5 | 16 | n |
93.5~99.5 | 3 | 0.06 |
(1)表中n= ,并在图中补全频数直方图.
(2)甲同学的比赛成绩是50位参赛选手成绩的中位数,据此推测他的成绩落在 分数段内;
(3)选拔赛时,成绩在93.5~99.5的三位选手中,男生2人,女生1人,学校从中随机确定2名选手参加全市决赛,请用列表法或树状图法求恰好是一名男生和一名女生的概率.
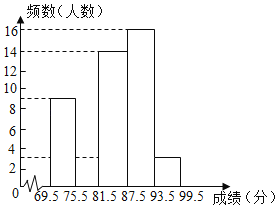
【答案】(1)0.32,补全频数直方图见解析;(2)81.5~87.5;(3)![]()
【解析】
(1)根据频率=频数÷总数求出m、n的值,从而补全图形;
(2)根据中位数的概念求解可得;
(3)利用列表或画树状图列举出所有的可能,再根据概率公式计算即可得解.
解:(1)n=16÷50=0.32,m=50×0.16=8,
补全图形如下:
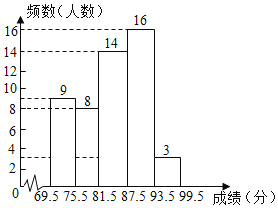
(2)由于共有40个数据,其中位数是第20、21个数据的平均数,
而第20、21个数据都落在81.5~87.5内,
∴推测他的成绩落在81.5~87.5分数段内,
故答案为:81.5~87.5.
(3)画树状图:
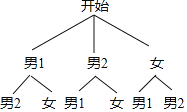
共有6种结果,其中一男一女的结果有4种,
∴恰好是一名男生和一名女生的概率为![]() =
=![]() .
.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD为矩形,曲线L经过点D.点Q是四边形ABCD内一定点,点P是线段AB上一动点,作PM⊥AB交曲线L于点M,连接QM.
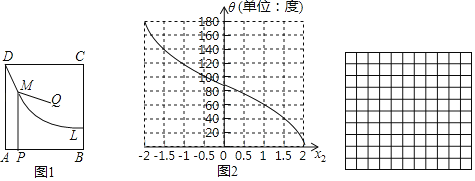
小东同学发现:在点P由A运动到B的过程中,对于x1=AP的每一个确定的值,θ=∠QMP都有唯一确定的值与其对应,x1与θ的对应关系如表所示:
x1=AP | 0 | 1 | 2 | 3 | 4 | 5 |
θ=∠QMP | α | 85° | 130° | 180° | 145° | 130° |
小芸同学在读书时,发现了另外一个函数:对于自变量x2在﹣2≤x2≤2范围内的每一个值,都有唯一确定的角度θ与之对应,x2与θ的对应关系如图2所示:
根据以上材料,回答问题:
(1)表格中α的值为 .
(2)如果令表格中x1所对应的θ的值与图2中x2所对应的θ的值相等,可以在两个变量x1与x2之间建立函数关系.
①在这个函数关系中,自变量是 ,因变量是 ;(分别填入x1和x2)
②请在网格中建立平面直角坐标系,并画出这个函数的图象;
③根据画出的函数图象,当AP=3.5时,x2的值约为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中直线y=x﹣2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).

(1)求反比例函数的关系式;
(2)将直线y=x﹣2向上平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,求平移后的直线的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 和点
和点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 是线段
是线段![]() 上的一个动点.设点
上的一个动点.设点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() 交抛物线于点
交抛物线于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
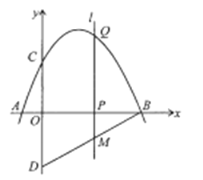
(1)求抛物线的解析式;
(2)连接![]() ,
,![]() ,当点
,当点![]() 运动到何处时,
运动到何处时,![]() 面积最大?最大面积是多少?并求出此时点
面积最大?最大面积是多少?并求出此时点![]() 的坐标;
的坐标;
(3)在第![]() 问的前提下,在
问的前提下,在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 值最小,求出
值最小,求出![]() 的最小值并直接写出此时点
的最小值并直接写出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() 是射线
是射线![]() 上一点,
上一点,![]() .动点
.动点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 水平向左作匀速运动,与此同时,动点
水平向左作匀速运动,与此同时,动点![]() 从点
从点![]() 出发,也以
出发,也以![]() 的速度沿
的速度沿![]() 竖直向上作匀速运动.连接
竖直向上作匀速运动.连接![]() ,交
,交![]() 于点
于点![]() .经过
.经过![]() 、
、![]() 、
、![]() 三点作圆,交
三点作圆,交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .设运动时间为
.设运动时间为![]() ,其中
,其中![]() .
.
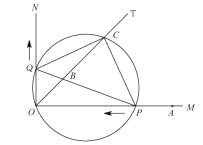
(1)求![]() 的值;
的值;
(2)是否存在实数![]() ,使得线段
,使得线段![]() 的长度最大?若存在,求出
的长度最大?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(3)求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,半径OC⊥AB于点O,点D是![]() 的中点,连接CD、OD.下列四个结论:①AC
的中点,连接CD、OD.下列四个结论:①AC![]() OD;②CE=OE;③△ODE∽△ADO;④∠ADC=∠BOD.其中正确结论的序号是( )
OD;②CE=OE;③△ODE∽△ADO;④∠ADC=∠BOD.其中正确结论的序号是( )
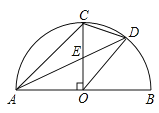
A.①④B.①②④C.②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,滑翔运动员在空中测量某寺院标志性高塔“云端塔”的高度,空中的点P距水平地面BE的距离为200米,从点P观测塔顶A的俯角为33°,以相同高度继续向前飞行120米到达点C,在C处观测点A的俯角是60°,求这座塔AB的高度(结果精确到1米).(参考数据:sin33°≈0.54,cos33°≈0.84,tan33°≈0.65,![]() )
)
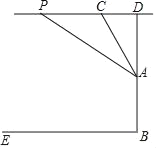
查看答案和解析>>
科目:初中数学 来源: 题型:
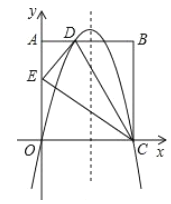
【题目】如图,在矩形![]() 中,点
中,点![]() . 沿直线
. 沿直线![]() 折叠矩形
折叠矩形![]() ,使点
,使点![]() 落在
落在![]() 边上,与点
边上,与点![]() 重合.分别以
重合.分别以![]() ,
,![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 轴建立平面直角坐标系,抛物线
轴建立平面直角坐标系,抛物线![]() 经过
经过![]() 两点.
两点.
(1)求![]() 及点
及点![]() 的坐标;
的坐标;
(2)一动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒
以每秒![]() 个单位长的速度向点
个单位长的速度向点![]() 运动, 同时动点
运动, 同时动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒
以每秒![]() 个单位长的速度向点
个单位长的速度向点![]() 运动, 当点
运动, 当点![]() 运动到点
运动到点![]() 时,两点同时停止运动.设运动时间为
时,两点同时停止运动.设运动时间为![]() 秒,当
秒,当![]() 为何值时,以
为何值时,以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?
相似?
(3)点![]() 在抛物线对称轴上,点
在抛物线对称轴上,点![]() 在抛物线上,是否存在这样的点
在抛物线上,是否存在这样的点![]() 与点 N,使以
与点 N,使以![]() ,
,![]() ,
,![]() ,
, ![]() 为顶点的四边形是平行四边形?若存在,请直接写出点
为顶点的四边形是平行四边形?若存在,请直接写出点![]() 与点
与点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
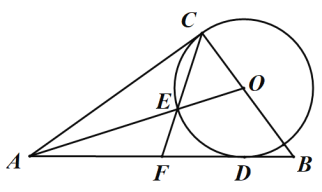
【题目】如图,在![]() 的边
的边![]() 上取一点
上取一点![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径画⊙O,⊙O与边
为半径画⊙O,⊙O与边![]() 相切于点
相切于点![]() ,
,![]() ,连接
,连接![]() 交⊙O于点
交⊙O于点![]() ,连接
,连接![]() ,并延长交线段
,并延长交线段![]() 于点
于点![]() .
.
(1)求证:![]() 是⊙O的切线;
是⊙O的切线;
(2)若![]() ,
,![]() ,求⊙O的半径;
,求⊙O的半径;
(3)若![]() 是
是![]() 的中点,试探究
的中点,试探究![]() 与
与![]() 的数量关系并说明理由.
的数量关系并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com