
【题目】在△ABC中,D、E分别是AB,AC的中点,作∠B的角平分线
(1)如图1,若∠B的平分线恰好经过点E,猜想△ABC是怎样的特殊三角形,并说明理由;
(2)如图2,若∠B的平分线交线段DE于点F,已知AB=8,BC=10,求EF的长度;
(3)若∠B的平分线交直线DE于点F,直接写出AB、BC、EF三者之间的数量关系。


【答案】(1)△ABC是等腰三角形,理由见解析;
(2)EF=![]() CG =1;
CG =1;
(3)EF=![]()
【解析】
试题(1)由三角形中位线的性质得DE∥BC,∠DEB=∠EBC,由BE平分∠ABC,得DE=DB,∠A=∠DEA,所以∠DEB+∠DBE+∠A+∠DEA=180°,∠AEB=90°,故△ABC是等腰三角形;(2)连接AF并延长交BC于点G,由DE∥BC,BF平分∠ABC,∠DFB=∠FBC,再由角边角得出△ABF≌△GBF,CG=2,由AE=CE得出EF =1;(3)分两种情况讨论.
试题解析:(1)△ABC是等腰三角形。
理由:∵D、E分别是AB,AC的中点,
∴DE∥BC ∴ ∠DEB=∠EBC,
∵BE平分∠ABC
∴∠DBE=∠EBC
∴∠DEB=∠DBE
∴ DE=DB
∵DE=DB=DA
∴∠A=∠DEA
∴∠DEB+∠DBE+∠A+∠DEA=180°
∴∠AEB=90°即BE垂直平分AC
∴BA=BC 即△ABC是等腰三角形
(2)连接AF并延长交BC于点G
∵D、E分别是AB,AC的中点
∴DE∥BC
∴ ∠DFB=∠FBC
∵BF平分∠ABC
∴∠DBF=∠FBC
∴∠DFB=∠DBF
∴ DF=DB
∵DF=DB=DA
∴∠DAF=∠DFA
∴∠DFB+∠DBF+∠DAF+∠DFA=180°
∴∠AFB=∠GFB=90°,BF=BF, ∠ABF=∠GBF
∴△ABF≌△GBF AB=GB=8,AF=GF
∴ CG=BC-BG=2
又AE=CE
∴EF=![]() CG =1
CG =1
(3) ①
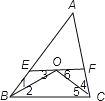
如图,∵EF∥BC,
∴∠2=∠3,
又∵∠1=∠2,
∴∠1=∠3,
∴OE=BE,
在△CFO中,同理可证OF=CF,
∵EF=EO+FO,
∴EF=BE+CF;
②
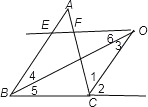
如图,∵OE∥BC,
∴∠5=∠6,
又∠4=∠5,
∴∠4=∠6,
∴OE=BE,
在△CFO中,同理可证OF=CF,
∵EF=EOFO,
∴EF=BECF.
综上:EF=![]()


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
【题目】甲,乙,丙三种作物,分别在山脚,山腰和山顶三个试验田进行试验,每个试验田播种二十粒种子,农业专家将每个试验田成活的种子个数统计如条形统计图,如图所示,下面有四个推断:
①甲种作物受环境影响最小;②乙种作物平均成活率最高;
③丙种作物最适合播种在山腰;
④如果每种作物只能在一个地方播种,那么山脚,山腰和山顶分别播种甲,乙,丙三种作物能使得成活率最高.其中合理的是( )

A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣2,﹣1,0,1,2,3这六个数中,任取一个数作为a的值,恰好使得关于x、y的二元一次方程组![]() 有整数解,且方程ax2+ax+1=0有实数根的概率是_____.
有整数解,且方程ax2+ax+1=0有实数根的概率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,锐角△ABC中,AD是高,E,F分别是AB,AC中点,EF交AD于G,已知GF=1,AC= 6,△DEG的周长为10,则△ABC的周长为( )

A. 27-3![]() B. 28-3
B. 28-3![]() C. 28-4
C. 28-4![]() D. 29-5
D. 29-5![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 于点
于点![]() ,点
,点![]() 为
为![]() 边的中点,过点
边的中点,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.
![]() 如图
如图![]() ,求证:四边形
,求证:四边形![]() 是矩形;
是矩形;
![]() 如图
如图![]() ,当
,当![]() 时,取
时,取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,在不添加任何辅助线和字母的条件下,请直接写出图中所有的平行四边形(不包括矩形
,在不添加任何辅助线和字母的条件下,请直接写出图中所有的平行四边形(不包括矩形![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
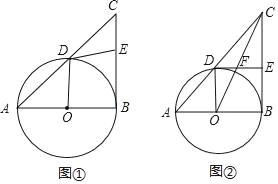
【题目】Rt△ABC中,∠ABC=90°,以AB为直径作⊙O交AC边于点D,E是边BC的中点,连接DE,OD.
(Ⅰ)如图①,求∠ODE的大小;
(Ⅱ)如图②,连接OC交DE于点F,若OF=CF,求∠A的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】指出下列问题中的总体、个体、样本:
(1)为了估计某块玉米试验田里的单株平均产量,从中抽取![]() 株进行实测;
株进行实测;
(2)某学校为了了解学生完成课外作业的时间,从中抽样调查了![]() 名学生完成课外作业的时间进行分析.
名学生完成课外作业的时间进行分析.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com