
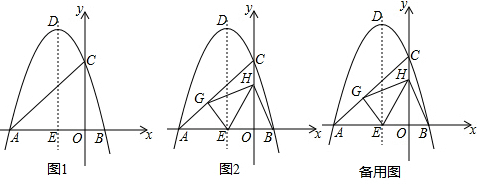
分析 (1)根据抛物线解析式可以得到点A、C的坐标,利用待定系数法可以求得直线AC的解析式;把抛物线解析式转化为顶点式方程,由此直接得到答案.
(2)作FQ⊥x轴于Q,交AC于点P.由一次函数和二次函数图象上点的坐标特征可以设F(m,-$\frac{1}{2}$m2+3m+8),则P(m,m+8).结合三角形的面积公式列出
S△ACF=-2(m+4)2+32,由二次函数最值的求法得到答案;
(3)如图3,连接BG交EH于点R,则BG⊥EH且BR=GR.作RK⊥x轴于点K,作GN⊥x轴于点N,由△BRE∽HOE得:$\frac{ER}{BR}$=$\frac{OE}{OH}$=$\frac{1}{2}$,则ER=$\sqrt{5}$.同理可得△RKE∽△HOE,易求EK=1,RK=2,OK=2.由△GNB∽△RKB可得:GN=2RK=4,NB=2KB=8,易求点G的坐标为(-6,4).则可得CG直线的解析式为y=$\frac{2}{3}$x+8.故设M(n,$\frac{2}{3}$n+8).所以MH2=$\frac{13}{9}$n2+$\frac{50}{3}$n+73,EH=3$\sqrt{5}$.此时可以对直角顶点进行分类讨论.
解答 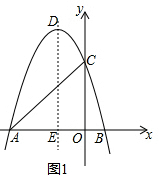 解:(1)如图1,∵y=-$\frac{1}{2}{x^2}$-3x+8=-$\frac{1}{2}$(x+8)(x-2),
解:(1)如图1,∵y=-$\frac{1}{2}{x^2}$-3x+8=-$\frac{1}{2}$(x+8)(x-2),
∴A(-8,0),B(2,0),C(0,8).
设直线AC的解析式为y=kx+8(k≠0),则
0=-8k+8,
解得k=1.
故直线AC的解析式为y=x+8.
又∵y=-$\frac{1}{2}{x^2}$-3x+8=y=-$\frac{1}{2}$(x+3)2+$\frac{25}{2}$,
∴D(-3,$\frac{25}{2}$);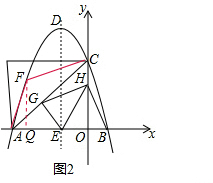 (2)设F(m,-$\frac{1}{2}$m2+3m+8).
(2)设F(m,-$\frac{1}{2}$m2+3m+8).
如图2,作FQ⊥x轴于Q,交AC于点P,则P(m,m+8).
∴PF=(-$\frac{1}{2}$m2+3m+8)-(m+8)=-$\frac{1}{2}$m2-4m(-8<m<0),
∴S△ACF=S△AFP+S△CFP=$\frac{1}{2}$FP•AQ+$\frac{1}{2}$PF•OQ=$\frac{1}{2}$PF(AQ+OQ)=$\frac{1}{2}$PF•OA=$\frac{1}{2}$(-$\frac{1}{2}$m2-4m)×8=-2(m+4)2+32,
∴当m=4时△ACF的面积最大,最大值为32,此时F(-4,2).
(3)存在,理由如下:
如图3,连接BG交EH于点R,则BG⊥EH且BR=GR.作RK⊥x轴于点K,作GN⊥x轴于点N,OE=3,OH=6,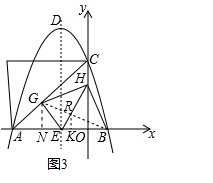 ∴EH=3$\sqrt{5}$.
∴EH=3$\sqrt{5}$.
∵EH•RB=BE•OH,
∴BR=2$\sqrt{5}$.
∵∠BER=∠HEO,∠BRE=∠HOE=90°,
∴△BRE∽HOE,
∴$\frac{ER}{BR}$=$\frac{OE}{OH}$=$\frac{1}{2}$,即$\frac{ER}{2\sqrt{5}}$=$\frac{1}{2}$,则ER=$\sqrt{5}$.
同理可得△RKE∽△HOE,
可得:EK=1,RK=2,OK=2.
由△GNB∽△RKB可得:GN=2RK=4,NB=2KB=8.
∴ON=6,
∴G(-6,4).
则可得CG直线的解析式为y=$\frac{2}{3}$x+8.
故设M(n,$\frac{2}{3}$n+8).
∴MH2=$\frac{13}{9}$n2+$\frac{50}{3}$n+73,EH=3$\sqrt{5}$.
此时可以对直角顶点进行分类讨论:
①当∠EMH=90°,存在点M的坐标为:M1(-3,6),M2(-$\frac{48}{13}$,$\frac{72}{13}$);
②当∠MHE=90°时,则M3(-$\frac{12}{7}$,$\frac{48}{7}$);
③当∠MEH=90°时,则M4(-$\frac{57}{7}$,$\frac{18}{7}$).
综上所述,符合条件的点M的坐标为:M1(-3,6),M2(-$\frac{48}{13}$,$\frac{72}{13}$),M3(-$\frac{12}{7}$,$\frac{48}{7}$),M4(-$\frac{57}{7}$,$\frac{18}{7}$).
点评 本题综合考查了一次函数、二次函数图象上点的坐标特征,抛物线的顶点公式,待定系数法求一次函数解析式,勾股定理以及三角形的面积求法等知识点.在求有关动点问题时要注意分析题意,分情况讨论结果.


科目:初中数学 来源:2016-2017学年广东省东莞市堂星晨学校七年级3月月考数学试卷(解析版) 题型:填空题
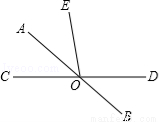
如图,直线AB、CD相交于点O,若∠BOD=40°,OA平分∠COE,则∠AOE= .
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com