
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径作⊙
为半径作⊙![]() ,
,![]() 为⊙
为⊙![]() 上一动点,连接
上一动点,连接![]() .以
.以![]() 为直角边作
为直角边作![]() ,使
,使![]() ,
,![]() ,则点
,则点![]() 与点
与点![]() 的最小距离为____.
的最小距离为____.
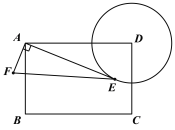
【答案】![]()
【解析】
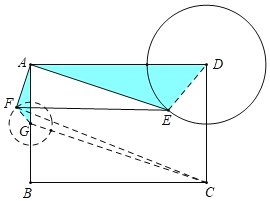
如图取AB的中点G,连接FG,FC,GC,由△FAG∽△EAD,推出FG:DE=AF:AE=1:3,因为DE=3,可得FG=1,推出点F的运动轨迹是以G为圆心1为半径的圆,再利用两点之间线段最短即可解决问题.
如图取AB的中点G,连接FG,FC,GC.
∵∠EAF=90°,tan∠AEF![]() ,∴
,∴![]() .
.
∵AB=6,AG=GB,∴AG=GB=3.
∵AD=9,∴![]() ,∴
,∴![]() .
.
∵四边形ABCD是矩形,∴∠BAD=∠B═∠EAF=90°,∴∠FAG=∠EAD,∴△FAG∽△EAD,∴FG:DE=AF:AE=1:3.
∵DE=3,∴FG=1,∴点F的运动轨迹是以G为圆心1为半径的圆.
∵GC![]() ,∴FC≥GC﹣FG,∴FC≥3
,∴FC≥GC﹣FG,∴FC≥3![]() 1,∴CF的最小值为3
1,∴CF的最小值为3![]() 1.
1.
故答案为:3![]() 1.
1.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
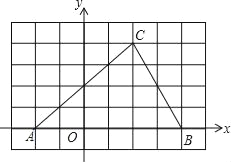
【题目】如图,在6×8的网格图中,每个小正方形边长均为1,原点O和△ABC的顶点均为格点.
(1)以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′与△ABC位似,且位似比为1:2;(保留作图痕迹,不要求写作法和证明)
(2)若点C的坐标为(2,4),则点A′的坐标为( , ),点C′的坐标为( , ),S△A′B′C′:S△ABC= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图抛物线![]() 交轴于点
交轴于点![]() ,交
,交![]() 轴于
轴于![]() (
(![]() 在
在![]() 左),且
左),且![]() ;
;
(1)如图![]() ,求抛物线的解析式;
,求抛物线的解析式;
(2)如图![]() ,在第一象限内抛物线上有一点
,在第一象限内抛物线上有一点![]() ,且点
,且点![]() 在对称轴的右侧,连接
在对称轴的右侧,连接![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,求出
,求出![]() 与
与![]() 的函数关系式(不要求写出自变量的取值范围);
的函数关系式(不要求写出自变量的取值范围);
(3)如图![]() ,在(2)的条件下,在点
,在(2)的条件下,在点![]() 右侧
右侧![]() 轴上有一点
轴上有一点![]() ,且
,且![]() ,连接
,连接![]() ,且
,且![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,点
,点![]() 是线段
是线段![]() 的延长线上一点,连接
的延长线上一点,连接![]() ,使
,使![]() ,取
,取![]() 中点
中点![]() ,在线段
,在线段![]() 上取一点
上取一点![]() ,射线
,射线![]() 与
与![]() 线段相交于点
线段相交于点![]() ,连接
,连接![]() ,在线段
,在线段![]() 上取一点
上取一点![]() ,连接
,连接![]() ,使得
,使得![]() ,若
,若![]() ,且
,且![]() ,求点
,求点![]() 的坐标.
的坐标.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应“学雷锋、树新风、做文明中学生”号召,某校开展了志愿者服务活动,活动项目有“戒毒宣传”、“文明交通岗”、“关爱老人”、“义务植树”、“社区服务”等五项,活动期间,随机抽取了部分学生对志愿者服务情况进行调查,结果发现,被调查的每名学生都参与了活动,最少的参与了1项,最多的参与了5项,根据调查结果绘制了如图所示不完整的折线统计图和扇形统计图.

(1)被随机抽取的学生共有多少名?
(2)在扇形统计图中,求活动数为3项的学生所对应的扇形圆心角的度数,并补全折线统计图;
(3)该校共有学生2000人,估计其中参与了4项或5项活动的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区2015年投入教育经费2900万元,2017年投入教育经费3509万元.
(1)求2015年至2017年该地区投入教育经费的年平均增长率;
(2)按照义务教育法规定,教育经费的投入不低于国民生产总值的百分之四,结合该地区国民生产总值的增长情况,该地区到2019年需投入教育经费4250万元,如果按(1)中教育经费投入的增长率,到2019年该地区投入的教育经费是否能达到4250万元?请说明理由.
(参考数据: ![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
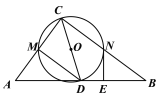
【题目】如图,在![]() △
△![]() 中,
中,![]() ,
,![]() 为斜边
为斜边![]() 上的中点,连接
上的中点,连接![]() ,以
,以![]() 为直径作⊙
为直径作⊙![]() ,分别与
,分别与![]() 、
、![]() 交于点
交于点![]() 、
、![]() .过点
.过点![]() 作
作![]() ⊥
⊥![]() ,垂足为点
,垂足为点![]() .
.
(1)求证:![]() 为⊙
为⊙![]() 的切线;
的切线;
(2)连接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,热气球的探测器显示,从热气球A看一栋大楼顶部B的俯角为![]() ,看这栋大楼底部C的俯角为
,看这栋大楼底部C的俯角为![]() ,热气球A的高度为270米,则这栋大楼的高度为______米
,热气球A的高度为270米,则这栋大楼的高度为______米![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】天猫商城某网店销售某款蓝牙耳机,进价为100元![]() 在元旦即将来临之际,开展了市场调查,当蓝牙耳机销售单价是180元时,平均每月的销售量是200件,若销售单价每降低2元,平均每月就可以多售出10件.
在元旦即将来临之际,开展了市场调查,当蓝牙耳机销售单价是180元时,平均每月的销售量是200件,若销售单价每降低2元,平均每月就可以多售出10件.
![]() 设每件商品降价x元,该网店平均每月获得的利润为y元,请写出y与x元之间的函数关系;
设每件商品降价x元,该网店平均每月获得的利润为y元,请写出y与x元之间的函数关系;
![]() 该网店应该如何定价才能使得平均每月获得的利润最大,最大利润是多少元?
该网店应该如何定价才能使得平均每月获得的利润最大,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,弦CD⊥AB,垂足为H.
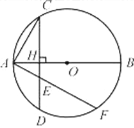
(1) 求证:AH![]() AB=AC2;
AB=AC2;
(2) 若过A的直线与弦CD(不含端点)相交于点E,与⊙O相交于点F,求证:AE![]() AF=AC2;
AF=AC2;
(3) 若过A的直线与直线CD相交于点P,与⊙O相交于点Q,判断AP![]() AQ=AC2是否成立(不必证明).
AQ=AC2是否成立(不必证明).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com