
分析 (1)根据正方形的面积为10可得正方形边长为$\sqrt{10}$,画一个边长为$\sqrt{10}$正方形即可;
(2)根据勾股定理和已知画出符合条件的三角形即可.
解答 解:(1)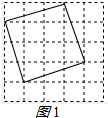 面积为10的正方形的边长为$\sqrt{10}$,
面积为10的正方形的边长为$\sqrt{10}$,
∵$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
∴如图1所示的四边形即为所求;
(2)∵$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,
∴如图2所示的三角形即为所求
这个三角形的面积=$\frac{1}{2}$×2×2=2;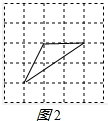
故答案为:2.
点评 本题考查了正方形的性质、勾股定理;熟练掌握正方形的性质,运用勾股定理得出有关线段长是解决问题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | -(-2)=-2 | B. | $({-3})×({-\frac{2}{3}})=6$ | C. | -34=(-3)4 | D. | (-1)2=12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).在图中作出△ABC关于y轴对称的△A1B1C1;
(1)如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).在图中作出△ABC关于y轴对称的△A1B1C1;查看答案和解析>>
科目:初中数学 来源: 题型:选择题
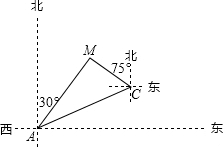 如图,某天然气公司的主输气管道从A市的北偏东60°方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市的北偏东30°方向,测绘员沿主输气管道步行1000米到达点C处,测得M小区位于点C的北偏西75°方向,试在主输气管道上寻找支管道连接点N,使到该小区铺设的管道最短,此时AN的长约是( )$\sqrt{2}≈{1.4^{\;}}{,^{\;}}\sqrt{3}≈1.7$.
如图,某天然气公司的主输气管道从A市的北偏东60°方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市的北偏东30°方向,测绘员沿主输气管道步行1000米到达点C处,测得M小区位于点C的北偏西75°方向,试在主输气管道上寻找支管道连接点N,使到该小区铺设的管道最短,此时AN的长约是( )$\sqrt{2}≈{1.4^{\;}}{,^{\;}}\sqrt{3}≈1.7$.| A. | 350米 | B. | 650米 | C. | 634米 | D. | 700米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 由3x-2=2x+1,移项得3x+2x=2+1 | |
| B. | 由$\frac{x-2}{2}$-$\frac{3x-2}{4}$=-1,去分母得2(x-2)-3x-2=-4 | |
| C. | 由2-3(x-1)=4,去括号得2-3x+3=4 | |
| D. | 由2x+3-x=5,合并同类项得3x+3=5. |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,二次函数y=ax2+bx+c图象的对称轴是x=$\frac{1}{3}$,下面四条信息:①abc<0,②a+2b+4c<0,③2a+3b=0,④2c>5b.你认为其中正确的有( )
如图,二次函数y=ax2+bx+c图象的对称轴是x=$\frac{1}{3}$,下面四条信息:①abc<0,②a+2b+4c<0,③2a+3b=0,④2c>5b.你认为其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com