
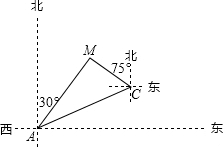
 如图,某天然气公司的主输气管道从A市的北偏东60°方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市的北偏东30°方向,测绘员沿主输气管道步行1000米到达点C处,测得M小区位于点C的北偏西75°方向,试在主输气管道上寻找支管道连接点N,使到该小区铺设的管道最短,此时AN的长约是( )$\sqrt{2}≈{1.4^{\;}}{,^{\;}}\sqrt{3}≈1.7$.
如图,某天然气公司的主输气管道从A市的北偏东60°方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市的北偏东30°方向,测绘员沿主输气管道步行1000米到达点C处,测得M小区位于点C的北偏西75°方向,试在主输气管道上寻找支管道连接点N,使到该小区铺设的管道最短,此时AN的长约是( )$\sqrt{2}≈{1.4^{\;}}{,^{\;}}\sqrt{3}≈1.7$.| A. | 350米 | B. | 650米 | C. | 634米 | D. | 700米 |
分析 首先过点M作MN⊥AC于点N,由题意可求得∠MAN=30°,∠MCN=45°,然后设MN=x,由三角函数的性质,可表示出AN与CN,继而可得方程:$\sqrt{3}$x+x=1000,解此方程即可求得答案.
解答 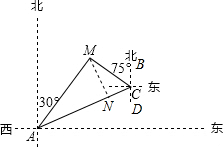 解:如图:过点M作MN⊥AC于点N,
解:如图:过点M作MN⊥AC于点N,
根据题意得:∠MAN=60°-30°=30°,∠BCM=75°,∠DCA=60°,
∴∠MCN=180°-75°-60°=45°,
设MN=x米,
在Rt△AMN中,AN=$\frac{MN}{tan30°}$=$\sqrt{3}$x(米),
在Rt△CMN中,CN=$\frac{MN}{tan45°}$=x(米),
∵AC=1000米,
∴$\sqrt{3}$x+x=1000,
解得:x=500($\sqrt{3}$-1),
∴AN=$\sqrt{3}$x≈650(米).
故选B.
点评 此题考查了方向角问题.此题难度适中,注意能构造直角三角形,并能借助于解直角三角形的知识求解是关键,注意数形结合思想与方程思想的应用.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:选择题
| A. | 6abc | B. | 6abc2 | C. | 12abc2 | D. | 36abc2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 数量x(个) | 1 | 2 | 3 | 4 | 5 |
| 售价y(元) | 8 | 16 | 24 | 32 | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=kx+b(b<0)的图象与反比例函数y=$\frac{π}{x}$的图象交于点P,点P在第一象限,PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交x轴、y轴于点C、D,且S△PAC=1,$\frac{OB}{OD}$=$\frac{1}{2}$,tan∠ACP=$\frac{1}{2}$.
如图,一次函数y=kx+b(b<0)的图象与反比例函数y=$\frac{π}{x}$的图象交于点P,点P在第一象限,PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交x轴、y轴于点C、D,且S△PAC=1,$\frac{OB}{OD}$=$\frac{1}{2}$,tan∠ACP=$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 32个 | B. | 36个 | C. | 38个 | D. | 40个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com