
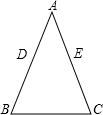
如图,在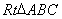 中,
中,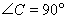 ,
,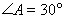 ,
,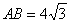 .若动点
.若动点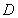 在线段
在线段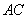 上(不与点
上(不与点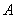 、
、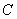 重合),过点
重合),过点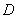 作
作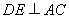 交
交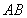 边于点
边于点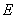 .
.
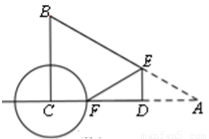
(1)当点 运动到线段
运动到线段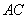 中点时,
中点时,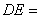 ?????? ;
?????? ;
(2)点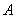 关于点
关于点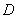 的对称点为点
的对称点为点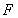 ,以
,以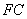 为半径作⊙
为半径作⊙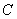 ,当
,当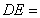 ????????? 时,⊙
????????? 时,⊙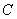 与直线
与直线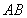 相切.
相切.
(1)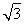 ??? (2)
??? (2)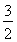 或
或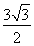 .
.
【解析】
试题分析:(1)求出BC,AC的值,推出DE为三角形ABC的中位线,求出即可;
(2)求出AB上的高,CH,即可得出圆的半径,证△ADE∽△ACB得出比例式,代入求出即可.
试题解析:(1)∵∠C=90°,∠A=30°,AB=4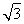 ,
,
∴BC=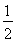 AB=2
AB=2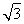 ,AC=6,
,AC=6,
∵∠C=90°,DE⊥AC,
∴DE∥BC,
∵D为AC中点,
∴E为AB中点,
∴DE=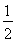 BC=
BC=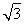 ,
,
(2)过C作CH⊥AB于H,
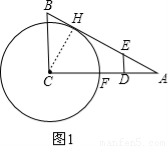
∵∠ACB=90°,BC=2 ,AB=4
,AB=4 ,AC=6,
,AC=6,
∴由三角形面积公式得: 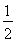 BC•AC=
BC•AC=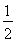 AB•CH,CH=3,分为两种情况:①如图1,
AB•CH,CH=3,分为两种情况:①如图1,
∵CF=CH=3,
∴AF=6-3=3,
∵A和F关于D对称,
∴DF=AD=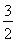 ,
,
∵DE∥BC,
∴△ADE∽△ACB,
∴ 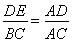 ,
,
∴  ,DE=
,DE=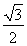 ;
;
②如图2,
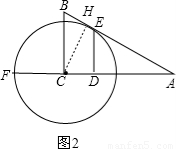
∵CF=CH=3,
∴AF=6+3=9,
∵A和F关于D对称,
∴DF=AD=4.5,
∵DE∥BC,
∴△ADE∽△ACB,
∴  ,
,
∴ 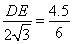 ,
,
DE=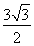 ;
;
考点: 1.切线的性质;2.含30度角的直角三角形;3.勾股定理;4.三角形中位线定理.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
 (2012•亭湖区一模)如图,△ABC中,AB=AC,若点D在AB上,点E在AC上,请你加上一个条件,使结论BE=CD成立,同时补全图形,并证明此结论.
(2012•亭湖区一模)如图,△ABC中,AB=AC,若点D在AB上,点E在AC上,请你加上一个条件,使结论BE=CD成立,同时补全图形,并证明此结论.查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在![]() 中
中![]() ,
,![]() 是
是![]() 的中点,以
的中点,以![]() 为直径的⊙
为直径的⊙![]() 交
交![]() 的三边,交点分别是
的三边,交点分别是![]() 点.
点.![]() 的交点为
的交点为![]() ,且
,且![]() ,
,![]() .
.
(1)求证:![]() .
.
(2)求⊙![]() 的直径
的直径![]() 的长.
的长.
(3)若![]() ,以
,以![]() 为坐标原点,
为坐标原点,![]() 所在的直线分别为
所在的直线分别为![]() 轴和
轴和![]() 轴,建立平面直角坐标系,求直线
轴,建立平面直角坐标系,求直线![]() 的函数表达式.
的函数表达式.

查看答案和解析>>
科目:初中数学 来源:2011-2012年北京西城外国语学校九年级第一学期期中考试数学卷 题型:解答题
如图,在 中,
中, ,
, .若动点
.若动点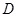 从点
从点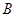 出发,沿线段
出发,沿线段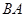 运动到点
运动到点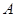 为止,运动速度为每秒2个单位长度.过点
为止,运动速度为每秒2个单位长度.过点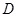 作
作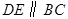 交
交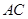 于点
于点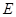 ,设动点
,设动点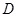 运动的时间为
运动的时间为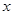 秒,
秒,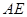 的长为
的长为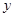 .
.

1.(1)求出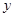 关于
关于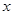 的函数关系式,并写出自变量
的函数关系式,并写出自变量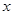 的取值范围;
的取值范围;
2.(2)当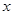 为何值时,
为何值时,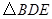 的面积
的面积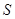 有最大值,最大值为多少?
有最大值,最大值为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com