练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知EF=CD=16cm，则球的半径为（　　）
    A．10$\sqrt{3}$cmB．10cmC．10$\sqrt{2}$cmD．8$\sqrt{3}$cm

    分析 首先找到EF的中点M，作MN⊥AD于点M，取MN上的球心O，连接OF，设OF=x，则OM是16-x，MF=8，然后在直角三角形MOF中利用勾股定理求得OF的长即可．

    解答 解：EF的中点M，作MN⊥AD于点M，取MN上的球心O，连接OF，
    设OF=x，则OM=16-x，MF=8，
    在直角三角形OMF中，OM2+MF2=OF2，
    即：（16-x）2+82=x2，
    解得：x=10．
    故选：B．

    点评 本题考查了垂径定理及勾股定理的知识，解题的关键是正确的作出辅助线构造直角三角形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    20．某电子商投产一种新型电子产品，每件制造成本为20元，在销售过程中发现，每月销量y（万件）与销售单价x（元）之间关系如表所示：
    销售单价x（元）212223242526
    月销量y（万件）18161412108
    （1）求每月的利润W（万元）与销售单价x（元）之间函数解析式；
    （2）当销售单价为多少元时，厂商每月能够获得最大利润？最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．如图，在△ABC和△DCB中，AB=DC，AC与BD相交于点E，若不再添加任何字母与辅助线，要使△ABC≌△DCB，则还需增加的一个条件AC=BD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．阅读材料，解答问题
    数学课上，同学们兴致勃勃地探讨着利用不同画图工具画角的平分线的方法．
    小惠说：如图1，我用相同的两块含30° 角的直角三角板可以画角的平分线．画法如下：
    （1）在∠AOB 的两边上分别取点M，N，使OM=ON；
    （2）把直角三角板按如图所示的位置放置，两斜边交于点P．
    射线OP是∠AOB的平分线．
    小旭说：我只用刻度尺就可以画角平分线．
    请你也参与探讨，解决以下问题：
    （1）小惠的做法正确吗？若正确，请给出证明，若不正确，请说明理由．
    （2）请你和小旭一样，只用刻度尺画出图2中∠QRS的平分线，并简述画图的过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，AD为△ABC的中线，BE 为△ABD的中线．
    （1）∠ABE=15°，∠BAD=40°，求∠BED的度数．
    （2）在△BED中作BD边上的高，垂足为 F．
    （3）若△ABC的面积为40，BD=5，则△BDE中BD边上的高EF的长为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．正△ABC的两条角平分线BD和CE交于点I，则∠BIC等于120°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．过多边形的一个顶点的所有对角线的条数与这些对角线分该多边形所得三角形的个数的和为21，求这个多边形的边数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

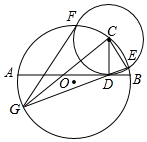    19．如图，AB是⊙O的直径，点C在⊙O上，⊙C与AB相切于点D，交⊙O于E、F两点，连接ED并延长交⊙O于G点，连接CG、FG．
    （1）求证：GC平分∠EGF；
    （2）求证：GD=GF；
    （3）若CD=3，求GD•DE的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

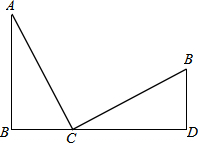    20．如图，B、C、D三点在同一直线上，∠ABC=∠CDE=90°，且AC⊥EC，BC=DE．
    （1）求证：△ABC≌△CDE；
    （2）若∠BAC=28°，求∠CED的度数．

    查看答案和解析>>

    同步练习册答案