Question

5．如图，AD为△ABC的中线，BE 为△ABD的中线．
（1）∠ABE=15°，∠BAD=40°，求∠BED的度数．
（2）在△BED中作BD边上的高，垂足为 F．
（3）若△ABC的面积为40，BD=5，则△BDE中BD边上的高EF的长为多少？

Answer 1

分析 （1）利用三角形外角和内角的关系，直接求出∠BED；（2）做△BED的BD边上的高就是过点E往BD所在的直线上做垂线；（3）因为中线把三角形分成面积相等的两个三角形，知△ABC的面积可求出△ABD的面积、△BDE的面积，利用三角形的面积公式，知底可求出该底上的高．

解答 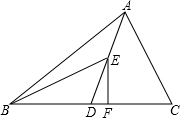解：（1）∵∠BED=∠BAD+∠ABE=40°+15°=55°；
（2）如右图所示：EF是BD边上的高．
（3）∵AD为△ABC的中线
∴S_△ABD=$\frac{1}{2}$S_△ABC=20
∵BE 为△ABD的中线
∴S_△BDE=$\frac{1}{2}$S_△ABD=10
EF=$\frac{2{S}_{△BDE}}{BD}$=4                           
所以△BDE中BD边上的高EF的长为4．

点评 本题考查了三角形的内外角关系、中线的性质及三角形的面积公式．三角形的外角性质：（1）外角等于不相邻的两个内角之和；（2）三角形的外角大于任何一个与它不相邻的内角；（3）外角和它相邻的内角互补．三角形的中线的性质：（1）三角形的三条中线相交于一点；（2）三角形的一条中线把三角形分成面积相等的两个三角形．